数学之中,有各种奇葩抽象的存在——公理啦、定理啦、命题啦……这一期,我们要说的,便是令无数数理科学家抓狂的————
悖 论
乌鸦悖论
乌鸦悖论,是二十世纪四十年代德国逻辑学家卡尔·古斯塔夫·亨佩尔(CarlGustavHempel;1905~1997)提出的。
悖论是这样的,
这位逻辑学家说:“乌鸦都是黑色的!”
这很正常,不是吗?
然后他说:“不是黑色的都不是乌鸦。”
这还是很正常,不是吗?
然后他说:“这两个命题是等价的!”
我们稍微用一下我们所学的知识:原命题与其逆否命题等价,就知道的确如此。
但是,你有没有在一瞬间觉得这两个命题好像有些不等价的感觉呢?
既然它们是等价的,那么我们对这两个命题的“信任程度”应当一致:
可 是!
A.每当你见到一只乌鸦,它是黑色的。显然这增加了你对命题“乌鸦都是黑色的”的信任程度。
B.当你见到了一只红苹果,它不是黑色的。它能增加你对命题“乌鸦都是黑色的”的信任程度吗?

我们的直觉告诉我们,这根本是两回事啊!
难怪有个诗人如此写道:

我从未见过紫色的牛,Ineversawapurplecow
但若我见到一头,ButifIweretoseeone
乌鸦皆黑的概率,Wouldtheprobabilityravensareblack
更加可能是一么?Haveabetterchancetobeone?
悖论,就这样产生了。

我们的亨佩尔先生提出这个悖论,目的在于说明归纳法违反直觉。换句话说,这个悖论在于,按照等价原理,我们对等价的两个命题本应有同样的信任度,但我们看到一个红苹果却只能增加“非黑色不是乌鸦”的信任度,而直觉上无法增加“乌鸦皆黑”的信任度。
细心的同学可能已经发现,导致悖论产生的原因,便是我们的直觉。 即用直觉衡量归纳推理的信任度是不够的。那么,我们应如何来衡量对一项归纳推理的“信任程度”呢?这就要引入概率推理的著名公式——贝叶斯公式(又称贝叶斯定理):
贝叶斯公式
贝叶斯公式是由英国数学家贝叶斯(ThomasBayes1702-1761)提出的,用来描述两个条件概率之间的关系,并且有着广泛的应用
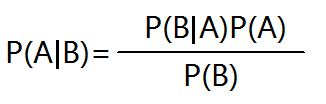
细心的同学可能已经发现,这不就是将条件概率公式用两遍然后拼在一起嘛?

ummmmm···
稍安勿躁,我们先来看它是怎么用的——
e.g.1:
一座别墅在过去的20年里一共发生过2次被盗,别墅的主人有一条狗,狗平均每周晚上叫3次,在盗贼入侵时狗叫的概率被估计为0.9,问题是:在狗叫的时候发生入侵的概率是多少?
解:设A事件为狗在晚上叫,B为盗贼入侵,则以天为单位统计,P(A)=3/7,P(B)=2/(20*365)=2/7300,P(A|B)=0.9,按照公式很容易得出结果:P(B|A)=0.9*(2/7300)/(3/7)=0.00058<<P(A|B)=0.9。
“狗吠盗来”≠“盗来狗吠”,你有没有想到呢?

e.g.2:
已知:

则

为多大呢?
解:根据贝叶斯公式,
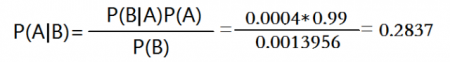
显然,P(A|B)=0.2837>>P(A)=0,0004,这生动形象地说明了“体测不及格说明人肥胖”是极其不靠谱的。

最后,我们来用它来说明乌鸦悖论中的两个命题的成立的概率是相同的:
设事件B=乌鸦,A=黑色,则由“乌鸦都是黑色的”可知,P(A|B)=1,
所以