1.花瓶OR美女脸

在上图中,你看见了什么?你看见的是两个美女脸,还是一个花瓶的轮廓?
同时感觉到两种有意义的图形是很困难的!!这是怎么回事?
这个Rubin花瓶/人脸图形是一个主体/背景可互换的两可图画。这是由于它既可以看成是白色背景上两张对视的黑色的美女脸,也可以理解为黑色背景上白色的花瓶。

Rubin花瓶/人脸两可错觉的起源于1915年,丹麦心理学家EdgarRubin使得这一“花瓶/人脸”的两可图形大扬其名,但追溯这一两可图形的家谱却远早于1915年。上面的那幅图形是斯坦福大学的心理学家RogerShepard所绘制。在这幅图形中,你可能看到的是两个女人的剖面图,也可能是一张烛台后模糊不清的脸孔。在此处,通常人们更多的看到的是一张脸而非两张脸。

荷兰画家M.C.Escher因其擅长画意义暧昧的图形/两可背景作品而闻名于世。
在18世纪法国的印刷品中,那些印刷品中的肖像画不仅描绘了通常自然状态下的花瓶,而且两个侧面像是不相同的,每个侧面像代表了一个特定的人。
2.左式错觉

你看到的褐色直线是平行的吗?
你也许会问:它们不是平行的,可这有什么大惊小怪的?可是事实上这些褐色直线是百分之百的平行!
它是如何形成的呢?早在60年代中期就有人根据轮廓形成的神经生理学知识提出了神经抑制作用理论,试图从神经生理学的角度来解释错觉,其中就包括左氏错觉。这种理论认为:当两个轮廓彼此接近时,它们在视网膜上的投影业彼此接近。由于视网膜上的神经细胞兴奋产生视觉信息时存在侧抑制现象(即相邻的感受细胞间存在互相抑制的现象),由轮廓所刺激的视细胞的活动被改变,使得神经兴奋的中心发生了相对的位移,进而引起几何图形形状和方向的错觉。
3.奇妙空间
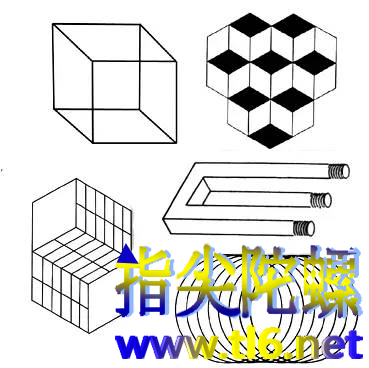
上面的图形也许是所有深度不明确的图形中最具代表性的,这种深度不明确的图形还有很多。
如果你稍微地注视这些图形中的任何一个,你将会感受到深度的倒转。在一些情况下,你将会感觉到方位的变化;在另一些情况下,立方体和分叉的数量会发生变化。在这种可变的情况下,你的大脑在某个时间只能感觉到一种图像,而不可能同时感觉到两种混合的图象。你的视觉系统被强迫地将一个平面的图形在感觉上感知为一个立体的图形。这些平面的图形使人们想到了立体的物体,但是这些图画也带有在深度知觉中可能会产生矛盾的线索。这些平面的图形是不稳定的,因为在现实的立体世界里,这些图形在两种不同的结构中是相等地存在的。当两种结构发生抵阻时,你就感觉到了一个不明确的、翻转的图形。
4.立体错觉(不可能的三角形)
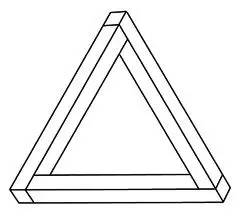
尽管这个不可能的三角形任何一个角看起来都是合情合理的,但是当你从整体来看,你就会发现一个自相矛盾的地方:这个三角形的三条边看起来都向后退并同时朝着你偏靠。但是,不知何故,它们组成了一个不可能的结构!我们很难设想这些不同的部分是怎么构成一个看似非常真实的三维物体的!其实,造成“不可能图形”的并不是图形本身,而是你对图形的三维知觉系统,这一系统在你知觉图形的立体心理模型时强制作用。在解释一幅三维图形的时候,你的视觉系统将会自动产生这一作用。
5.大小恒常性错觉

在上面一幅图像中,一个大个子正在追赶一个小个子,对不对?
其实,这两个人完全是一模一样的!(不信?用尺子量量看!)你所看见的并不一定总是你所感知的。
对于这种错觉,斯坦福大学的心理学家RogerShepard认为它与三维图像的适当的深度知觉有关。与这有关的是,后面的那个人看起来比前面的那个人离你远些,但不管怎样,后面的那个人在实际尺寸上与前面那个人是一样大的。
通常一个东西离你越远,它就显得越小,换句话说,它的视角变小了。在这幅图里,后面的图形与前面的图形有着相同的尺寸(和相同的视角)。由于两个图形的视觉相同而距离不同,因此,你的视觉系统就会认为后面的那个人一定比前面的大。这个例子说明了你所看见的并不一定是你所感知的。
6.填充错觉

看看这幅图,中间有一个黑点,周围是一团灰雾。盯着黑点目光不要移动,是不是觉得灰雾消失了!
同样的你试试下边的那幅,这次灰雾不会消失了。这是怎么回事?为什么灰雾有时消失有时又不消失?

这是怎么回事?!
我们的眼睛不习惯于固定的刺激,视觉中有一个系统调节眼球的运动使物体的视像保持在视网膜上的某个固定的区域,我们将这个系统称之为视觉稳定系统。
你可以通过后像来体验这种视觉稳定的效果。如果你盯着一个物体看上一分钟,移走目光后它的后像仍会在眼前停留几秒种,然后才会消失。你可以通过眨眼使其多停留一会儿。
现在再来看看最上边的那幅图,大多数人当他们凝视黑点的时候都感到灰雾消失了,而对下边的那幅灰点不会消失。在最上边的图里,从中心的黑点向外灰雾逐渐由黑变浅,这种渐变与视觉的停留过程是一致的,当然如果你的目光随意移动的话,灰雾的视像一直保留在视网膜上。当你注目盯着黑点时,灰雾逐渐减弱直到消失,而背景的颜色取而代之。
7.螺旋错觉(螺旋or同心圆)


你在左图可以看到Fraser螺旋。黑色的一圈圈的弧看起来是一个螺旋,其实它们是由一组同心圆构成。看右图,这种幻觉逐渐不明显了。如果你用手遮住上图的上半部分,这种幻觉不复存在。这意味着知觉上的特性必然产生此种效应。
这种Fraser螺旋错觉是最复杂的盘旋绳索错觉,许多因素导致了这种视觉上的错觉。因此,即使这些同心圆本身的轨迹暴露了,背景上每一个带有方向性的小单元格仍使之产生螺旋上升的知觉。
这种错觉的形成是因为多变的背景,你会发现右图的错觉不是很明显了,只是因为背景改变了,但它确实还存在。这些带有方向性的小单元格分组聚合,使螺旋路径明显。
8.缪勒-莱耶错觉
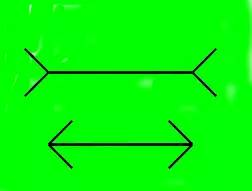
看看上面的带箭头的两条直线,猜猜看哪条更长?
是上面那条吗?
错了!其实它们一样长。
这就是有名的缪勒--莱耶错觉,也叫箭形错觉。
它是指,两条长度相等的直线,如果一条直线的两端加上向外的两条斜线,另一条直线的两端加上向内的两条斜线,则前者会显得比后者长得多。
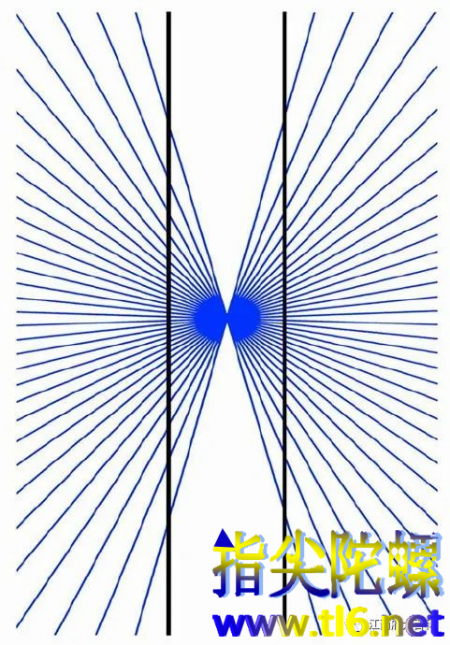
9.黑林错觉

平行的黑线完全是笔直而平行的,放射线会歪曲人对线条和形状的感知,这种经典幻觉由19世纪初德国心理学家艾沃德·黑林首先发现。此图属于“黑林错觉”。并在当时用于研究人眼对错觉的判断,到19世纪末曾试用于审判犯人。这种错觉的具体原理尚在研究中。
10.贾斯特罗错觉

贾斯特罗错觉〔Jastrowillusion〕是指两条等长的曲线,包含在下的一条比上面一条看上去会长一些;同样,两个完全一样的扇形环,包含在下面的扇形环比上面的扇形环看上去大些的视错觉现象。
圆内外圈半径不等,角度相同,弧长不等。在比较物品大小时,人会不自觉的用两个物品相邻的两边来做比较,进而将长边和短边进行比较,大脑就会将拥有较长的一边物体分辨成比较大的那一个了。


(名侦探柯南中的贾斯特罗错觉)
11.蓬佐错觉

蓬佐错觉是一种视错觉(又称“铁轨错觉”、“月亮错觉”),最早由意大利心理学家马里奥·蓬佐(MarioPonzo,1882-1960)说明。他认为人类的大脑根据物体的所处环境来判断它的大小,他通过画出两条完全相同的直线穿过一对向某点汇集的类似铁轨的直线向人们展示这种错觉。上面那条直线显得长一些是因为我们认为根据直线透视原理那两条汇集的线其实是两条平行线逐渐向远方延伸。在这种情况下,我们就会认为上面那条线远一些因此也就长一点,因为如果远近不同的两个物体在视网膜上呈现出相同大小的像时,距离远的物体在实际上将比距离近的物体大。
12.格里德火花错觉

格里德火花错觉是指人眼在看见一张网格图,感觉每一个格点都有一个小圆时,但盯着格点看,小圆点又消失了
又如下图,盯着看时,是静止的,但感觉上却是运动的