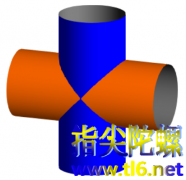
牟合方盖
中华文化博大精深,提到中国古代数学,不得不提牟合方盖,下面一探究竟。
笔者应公众号留言,尝试以GeoGebra做了一个“牟合方盖”,老师们有兴趣可以参考,也可以到文章末尾下载源文件参考,制作过程见本文最后视频.
牟合方盖效果如下:

下面我们一起来叭叭“牟合方盖”的历史。
01
九章算术“开立圆术”
我国著名的数学典书籍《九章算术》中记载了求已知体积的球体直径的方法,称之为“开立圆术”,“立圆”即为球体。

所谓“开立圆术”,书中载曰:“置积尺数,以十六乘之,九而一,所得开立方除之,即丸径。”意思是说球体的半径等于九分之十六乘以体积再开立方,与此同时,也就得出了球的体积公式:十六分之九乘以半径的三次方。
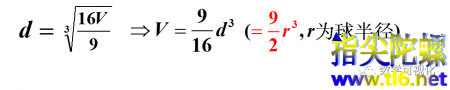
古人认为,圆周率约等于3,也就是圆周长是圆半径的三倍。从经验中得到下面的图形中,圆柱体积:球的体积=4:3
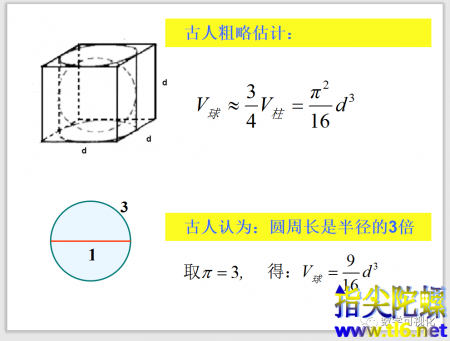
当然,我们一眼就可以看出这个公式是错误的。可是我们应该知道任何一个数学公式,无论看起来多么简单,都是一代代数学家不多努力而得到的劳动成果。
02
刘徽的纠错
刘徽,魏晋时期伟大数学家。著有《九章算术注》和《海岛算经》。他于公元263年撰《九章算术注》

刘徽
就在他为《九章算术》做注的时候,发现上述推理过程中的错误,即“圆柱体积:球体积=4:3”是错误的。当时刘徽已经推算出圆周率为3.1416。为了解决球体积的问题,他构思了一个看似奇葩,却有确实有效的物体,它叫做“牟合方盖”。
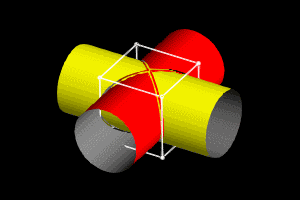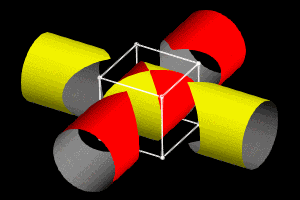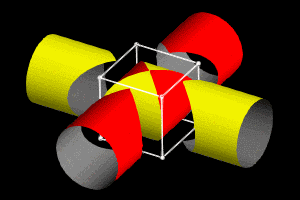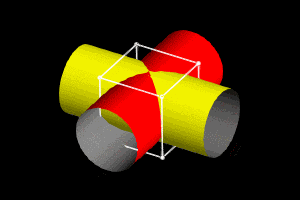
这里的“牟”意思是相同。“盖”意思是伞。“牟合方盖”就是指两个面合在一起的两个相同的方伞。它是由一个正方体出发,先用竖直方向的内切圆柱截正方体,得到一个圆柱体,再用水平方向的圆柱再截一次,两个圆柱的共同部分所形成的几何体,就叫做“牟合方盖”。

看似容易的一个方盖,这一创举足以让刘徽名垂青史,“牟合方盖”恰好把正方体的内切球包含在内,并且二者是相切的关系。如果用一个水平面去截方盖,会得到一个正方形和一个内切圆,二者的面积比例是4:π。从而得到“方盖”和“球”的体积之比是4:π。现在所有的工作重心落在了如何求出“牟合方盖”的体积,一旦求出该体积,球的体积瞬间即可攻破!
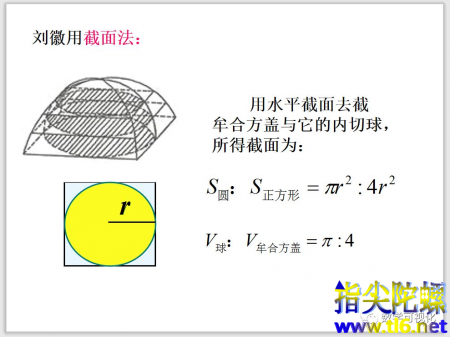
但是刘徽没有解答出来。留下一段话:“观立方之内,合盖之外,虽衰杀有渐,而多少不掩.判合总结,方圆相缠,浓纤诡互,不可等正.欲陋形措意,惧失正理.敢不阙疑,以俟能言者.”
翻译过来就是:“我弄不了了,谁行谁上吧!”
03
祖冲之与祖暅接棒
解决此问题的人便是南北朝时期杰出的数学家袓冲之及他的儿子祖暅。

祖冲之
祖冲之(429--500),中国南北朝时期杰出的数学家、天文学家和机械制造专家,祖籍今河北省涞源县.祖冲之的壮举我们都晓得:将圆周率精确到了小数点后7位。
祖暅,也是著名的数学家和天文学家,继承和发展了其父亲的科学事业.《缀术》是他们父子完成的数学杰作.祖暅有一个原理我们很熟悉:
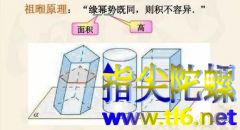
祖暅原理:“幂势既同,则积不容异”。“幂”是截面积,“势”是立体的高。意思是两个同高的立体,如在等高处的截面积相等,则体积相等。更详细点说就是,界于两个平行平面之间的两个立体,被任一平行于这两个平面的平面所截,如果两个截面的面积相等,则这两个立体的体积相等。上述原理在中国被称为祖暅原理,国外则一般称之为卡瓦列利原理。
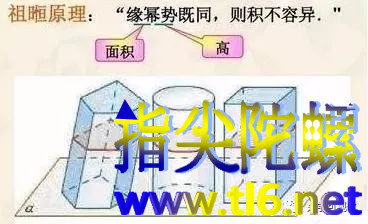
牟合方盖这一几何体的体积怎么求呢?刘徽等了200多年,终于等到了“能言者”,祖冲之和他儿子祖暅终于解决了牟合方盖的体积。只需要找到一个和“牟合方盖”体积相同的几何体,这个几何体需要满足两个条件:①简单易求,②与方盖满足“幂势既同,则积不容”。
把“牟合方盖”进行8等分,我们把它称之为8个“小方盖”,切割方法是:俯视方盖,横竖两刀,正视方盖,横着来一刀。
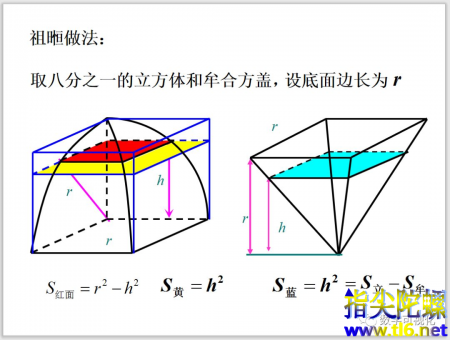
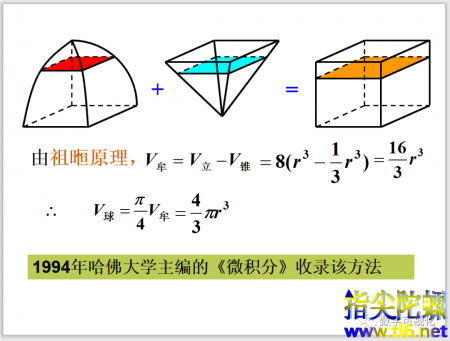
不得不说,这在当时是相当先进的数学技法!
04
外国的相关探究
国外也有关于球体积的公式获得。比如阿基米德通过力学原理和穷竭法推导,读者感兴趣可以关注公众号,回复“牟合方盖课件下载”,找到相关文档。
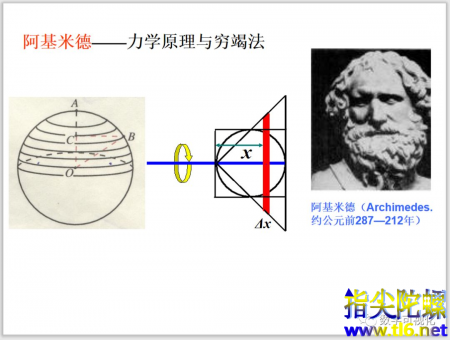
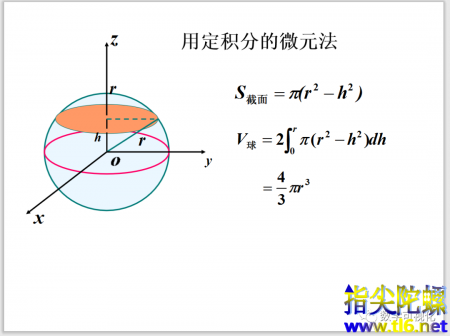
当然后期还有更先进的微元法。