1祖暅原理与球体体积计算
这篇文章提了一些值得大大商榷、似是而非的观点。例如
数学教育领域有一个共识,就是一个现代人学习数学的历程大体上沿着数学发展史的历程,类似于一个胎儿成长的过程大体上沿着生物进化的历程。因此,判断一般人(尤其是中学生)的数学水平的基本标准是历史的,即看他懂的是哪个时代的数学。为说明这些观点,原文作者先用解析几何与平面几何的关系作为例子,评论道
即使对于很好的学生,像上面那样做平面几何难题也应适可而止,有精力和兴趣可早些进入解析几何,那么以前学的很多方法和技巧即使忘掉也没有关系,不需要全都记住而成为沉重的负担。这就是“由厚到薄”的过程。接着原作者举了一个例子:
再举个例子:球的体积怎样算?在高中教科书中是用祖暅原理计算的。祖暅原理本身就不很容易懂,而利用祖暅原理计算球的体积,需要相当高的技巧,实际上大多数高中生没学明白。更大的问题是,如果换一个计算体积的问题,还得再寻求新的方法,无法保证一定能算出来。但是,如果学了微积分就会算很多面积、体积,其中球的体积只是一个很容易的问题。这样,学了微积分就可以“忘掉”很多计算面积、体积的初等方法和技巧,这也是“由厚到薄”的过程。作者的意图,是想说解析几何比平面几何更近代,从而更高等;微积分比祖暅原理更近代,更高等。
但是,作者忽视了平面几何的价值,忽视了古人计算球体体积的价值,以为有了解析几何就包打天下,学会了微积分就比祖暅的数学水平更高,实在是数祖忘典。
我们姑且批评逐句批评下上面涉及祖暅原理与球体体积的计算的那段文字。
文章说祖暅原理不容易理解。这是真的吗?事实上,祖暅原理很简单。

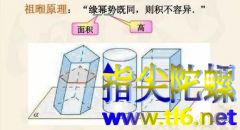
祖暅(公元前5-6世纪)是我国著名数学家祖冲之的儿子。他提出(后人总结,刘徽、祖冲之都有类似的思想):“夫叠棋成之积,幂势既同,则积不容异。”这里的“幂”指水平截面的面积,“势”指高。也就是说,等高的立体,如果每个截面的面积相同,则这两个立体有相同的体积。这个思想通过下面的堆积的硬币图形可以直观理解。

说祖暅原理不易理解,是把简单的数学原理、数学思想故意拔高到吓人的高度,让数学变得不亲民。文章说学了微积分就可以“忘掉”很多之前计算面积、体积的初等方法。显然,作者认为用祖暅原理计算是初等方法,是可以忘掉的。殊不知,祖暅原理是微积分中计算体积的必不可少的。计算体积要算重积分,重积分往往化为累次积分来算(Fubini定理),这其中就用到祖暅原理。在西方,直到17世纪才由意大利几何学家卡瓦列里(Cavalieri,1598年-1647年)提出类似的原理,所以西方往往称该原理为卡瓦列里原理。但卡瓦列里原理的提出比中国的祖暅原理晚1千多年。

在意大利,卡瓦列里是一位有纪念雕像,备受尊重的数学家。中国人也不该忘却祖暅。另外,祖暅原理实际蕴涵了微积分的思想,即体积(或面积)的计算可以由计算许多个小体积(面积)之和而得到。文章说利用祖暅原理计算球体体积的方法,“实际上大多数高中生没学明白。”这是过多担心高中生的理解能力和学习能力了。
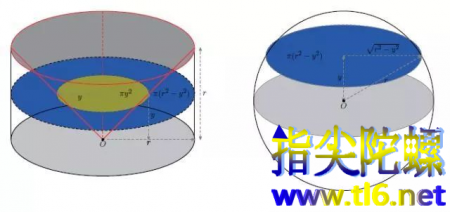
原文说学了微积分,很多体积计算问题更容易。实际上,这并不是因为放弃了祖暅原理,反而恰恰是因为用了祖暅原理,再加上了伟大的牛顿-莱布尼兹公式。原文说“如果换一个计算体积的问题,还得再寻求新的方法,无法保证一定能算出来。”在微积分发明之前,对不同的体积计算问题,祖暅原理不需要更换,万变不离其宗,变的只是要不同的方法算横截面面积。
原文作者以为用祖暅原理计算了球体体积的计算,不如微积分可以计算更多立体的体积。大大不然。球体体积的计算在数学史上有重要的地位。前面卡瓦列里的雕像的手中握着的就是一个球,古希腊最伟大的数学家阿基米德的坟墓前也有圆柱容球的雕像。祖冲之用祖暅原理和古人独创的牟合方盖,计算出球体体积,足以与西方的数学交相辉映。
古人的智慧,不是懂了微积分的现代人就可以藐视的。

我们以为原文作者忽视了数学史在数学教育中的价值而简单粗暴地以为使用面更广的工具可以替代较早的内容。
2集合论为说明我们不是抓住一点不放,不够宽容,我们再简单批评下原文对集合论的一些观点。
原文有如下文字:
但群是无法回避的,因为它在数学中处于核心地位。由此集合论也就发展起来(实际上到20世纪才成熟),进而成为整个数学的一种方便的语言。集合论是康托尔创立的,康托尔研究集合论是因其研究分析问题而开始的,不知作者为何说集合论是因为对群论的研究而发展起来的。
另外,原文质疑了在中学数学教程中是否应该讲“集合”,他说:
其一,引入集合的语言不过是为了讲课方便,但可能是老师方便了学生苦了(因为“集合”比方程、直线等更抽象,因而对于很多学生更费解);
其二,集合概念对于学习中学数学的各课题都不是必需的(早年的中学数学教程中都没有集合,但同样可以讲得很好,而且并不影响学生的数学素质);
其三,如果没有实质性的应用,花了很多时间学习“集合”却不能得到什么实际的好处,是很大的浪费(学生质疑“有什么用”的一个主要对象就是集合);
其四,在中学课程中不可能系统地讲清集合论的基本概念,至多只是“朴素直观”而已,但这样的直观是不严谨的(在这方面,数学界也只是在罗素发现“集合论悖论”后才明白)。
集合论作为数学的基础,有些妄人反对在大学讲,现在第一次看到有人反对在中学讲。贸然质疑中学讲集合论是不负责任的。我们简单逐条反驳如下:
其一,原文作者以为集合论使学生费解。但更抽象,更费解就不能讲了?数学的一个重要价值不就是培养学生的抽象能力吗?
其二,原文作者以为集合论不是必需的。现在中学的许多内容,如几何学,如解方程,如初等概率论,是集合论发展起来以前的知识,自然可以不用集合论。但我们不妨以子之矛攻子之盾:原文作者提倡近代的数学内容更高等,为何近代发展起来的集合论不是好的更方便的工具和语言?
其三,原文作者质疑集合论没有实质性的好处。且不谈集合论的语言在中学数学中几乎无处不在,如不等式的解集,运动质点的点集等等,就谈集合论与现代数学相衔接这一点上,如集合论是概率论的基础,就是极大的好处。
其四,原文作者以为在中学不能讲清楚集合论的基本概念就不能讲了。其实数学学习中,很多基本概念讲不清就进行下去了。如中学能讲清楚实数吗?不能,但还不是在学?大学初等概率论中,随机变量就是一个一般课堂没法讲清楚的概念,背后需要用到严格的测度论知识。随机变量函数的期望的计算方法也是没法讲清楚的。但又有谁说,既然讲不清,我就不学了呢?
3数理统计原文还讨论到数理统计:
统计学原来也属于文科,那时并没有严格的科学方法,所用到的数学很初等。直到1930年代概率论奠定基础后,产生了“数理统计”这个新学科,从此统计有了科学的研究方法,从根本上改变了统计学的面貌。这段话也值得商讨。在概率论发展起来之前,统计学已经有了很大的发展。无须提及高斯的最小二乘法和正态分布在1930年代之前。此外,皮尔逊于1900年提出检验拟合程度的
统计量和
分布,建立了
检验法。1908年,英国科学家W.S.戈塞特导出大统计量及其精确的分布,建立了
检验法。
4结束语
因为没有读全文,对原文的其他观点,我们暂不予评论。但如果一篇文章漏洞太多,就很令人怀疑其他观点的是否值得去了解。
虽然我们对作者的文章内容有所批评,但我们认为,加强数学教育,还是有必要的,否则就会出现一些可笑的文章,参考
数学能力不强导致的妄想|评南科大刘洋博士科幻作品《勾股》
“返朴”不可谓不专业:著名物理学家文小刚,当红女科学家颜宁院士联袂总主编,丁玖等数学专业人士任编委。但从上面的讨论可见,该号还需加强采编的专业性。读者可参考阅读本号批评丁教授文章的文章:
批判|美国的微积分教学方式一定好吗?
当然,匆忙之中,我们的批评也一定有不严格处。我们期待抛砖引玉,有更多的有益的讨论。