圆和球还是最实用的图形。宏大如宇宙天体,微小至原子电子,飞转的车轮,滴嗒的钟表……人们的日常生活离不开圆和球,科技的进步也离不开圆和球。
简单中寓深奥。在圆与球简约的外形下,潜藏着无穷的数学奥秘。
圆周长和圆面积的计算,蕴涵着极限思想。中国古代数学家刘徽创立的“割圆术”,就是用圆内接正多边形去逐步逼近圆。刘徽从圆内接正六边形出发,将边数逐次加倍,并计算逐次得到的正多边形的周长和面积(以及相应的圆周率近似值)。

纪念割圆术的邮票
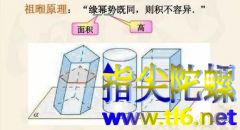
古希腊数学家称用多边形逼近曲线图形的方法为“穷竭法”,早在公元前3世纪,阿基米德也是用这种方法去计算圆的周长、面积及圆周率的。不过阿基米德最引以自豪的,是他对球体积的计算。阿基米德考虑一个球和它的外切圆柱,以及一个辅助的圆锥,其基本做法是将这些立体分割成无数的薄片,并用力学平衡的方法比较它们的体积,最后求得球体积的正确公式:(R是球半径)。阿基米德的方法可以看成是积分学的先声。无独有偶,在东方,中国南北朝时期的数学家祖冲之和他的儿子,也是利用球和它的外切圆柱计算出正确的球体积公式。不过与阿基米德不同,祖氏父子考虑的是同一个球的两个互相垂直的外切圆柱的公共部分(刘徽最先发现该种立体并命名为“牟合方盖”),并运用欧洲学者迟至17世纪才重新发现的不可分量原理推算出这部分立体与其所含内切球的体积之比。祖氏父子的方法与阿基米德的可以说是异曲同工,殊途同归。
至于近代微积分的发明,圆和球也扮演了重要的角色。我们知道,在17世纪上半纪微积分酝酿时期,圆面积与圆周率π的计算,曾是那些寻找打开无穷小算法大门钥匙的数学大师们关注的热点。牛顿之前的先行者、英国数学家沃利斯在其代表作《无穷算术》中,用插值法计算1/4圆的面积,并进而导出了无穷乘积表达式。

沃利斯
牛顿推广沃利斯的方法而得到了指数可以是分数和负数的二项定理,二项定理在建立微积分算法中的作用是众所周知的。在解析几何的发明人笛卡儿手中,圆是他作图求解方程的基本工具。笛卡儿在《几何学》一书中提出的求曲线切线的方法甚至以“圆法”著称,而牛顿正是从研究、改善笛卡儿“圆法”开始踏上制定微积分的漫漫征途。微积分的另一位发明人莱伯尼茨也计算过圆面积及圆周率,他给出了π的无穷级数表达式。

笛卡尔纪念邮票
饶有意味的是,与牛顿、莱布尼茨差不多同时代的日本“算圣”关孝和,开创了独具一格的“圆理”。他所谓的“圆理”,即指与圆有关的研究,以无穷级数为基础,计算各种曲线与曲面围成的图形之面积与体积,说明当时东方的数学家们也在竭力用圆这把钥匙叩击着微积分的大门。
古希腊“数学之神”阿基米德把球体积推算视为他一生最得意的成果,曾留下遗嘱把球及其外切圆柱的图形刻在他的墓碑上。阿基米德在第二次布匿战争期间被罗马士兵杀害,据传当罗马军士冲到阿基米德身边时,这位正在思考数学问题的老人喊出的最后一句话是:“别动我的圆!”阿基米德死后,罗马军队的主帅马塞吕斯下令为阿基米德隆重建墓,并遵照阿基米德的遗愿,在他墓前竖了一块石碑,墓碑上刻着的正是那不朽的图形—球及其外切圆柱。记载着阿基米德球体积计算的羊皮书手稿,历经千年尘封后终于重见天日,被誉为20世纪最重大的考古发现而轰动一时。

阿基米德的墓碑上就刻着他一生最得意的发现
"圆柱容球"的几何图形
至于圆周率π的计算,这方面的成就往往被用作衡量某一时代、某一地区文化水平的标征。前面已提到的祖冲之,亦以圆周率的计算而彪炳史册。据《隋书》记载,祖冲之算出圆周率的精确值在3.1415926与3.1415927之间,这在公元5世纪时创造了世界之最。为了纪念这位文化名人,人们把月球上的一座环形山命名为“祖冲之山”。1955年,中国还发行了祖冲之纪念邮票。祖冲之并不是仅有的出现在邮票上并与圆周率有关的数学家。伊朗曾发行过纪念阿拉伯数学家阿尔·卡西的邮票,阿尔·卡西恰恰是祖冲之之后刷新圆周率计算记录的第一人,他在公元14世纪,给出了准确到13位小数的圆周率近似值。今天,电子计算机已经将数值计算到小数点后数万亿位。然而,电子计算机的发明、使用本身离不开圆的数学。
我们已经看到,圆与球,简单,美丽,奥妙,述说着一个跨时代、跨文化的数学故事。最后,让我们回到本文开始之处—北京天坛,去侧耳倾听沿着那圆形的回音壁回荡的永恒的“圆舞曲”吧。