今天简单介绍一下对数螺线及其绘制方法。
还有一些与对数螺线非常接近的“螺线”。
首先讲一下黄金矩形。
宽与长的比值等于黄金比0.618···的矩形称为黄金矩形。
黄金矩形的一个特点是,沿着与短边平行的方向,从黄金矩形中一刀切掉一个边长等于宽的正方形,所剩的图形是一个与原来矩形相似的黄金矩形。
这一过程可以无限地进行下去。
并且,如果按照一定的顺序有规律地切割(比如下图中是从矩形右侧切掉一个正方形,然后把剩余矩形顺时针旋转90°,然后重复前面的动作),最终,这一串黄金矩形的极限将是一个点。
容易证明,这个点正好就是前两个黄金矩形对角线的交点。
如下图所示。
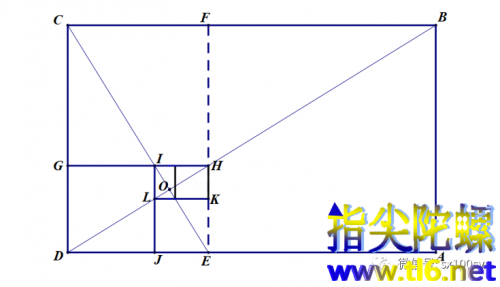
具体来说,矩形ABCD就是黄金矩形(CD:DA=0.618···),从它上面切掉正方形ABFE后,剩余一个矩形DEFC仍然是黄金矩形。
继续这样进行下去,黄金矩形将形成一个从大到小的矩形序列,这个序列最终收缩到一点,即图中的点O。
点O是矩形ABCD的对角线DB与矩形DEFC的对角线CE的交点。
也是矩形DEFC的对角线CE与下一个矩形EHGD的对角线DH的交点,······。
如果我们在每个正方形中依次作一个四分之一圆弧,将得到一条“螺线”。
但且慢,这样画出来的“螺线”其实不是真正的螺线。
我们来分析一下为什么不是。
如下图所示,这条看似的“螺线”从点A开始,路径是:
A→F→G→J→K→M→N→P→···→O(蓝线)
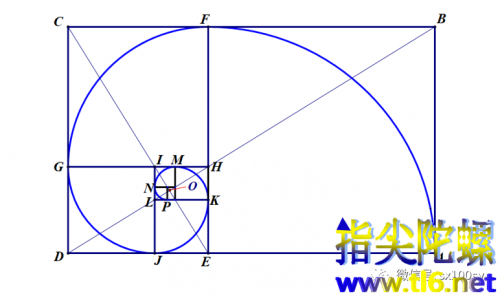
可以看出,这条螺线的曲率越来越大(更加弯曲,也就是曲率半径越来越小)。
但其实,这条螺线的曲率的变化却是有间断或跳跃的,是一种阶梯状。
这是因为每一段四分之一圆弧的曲率不变但互相都不相同。
间断发生在相连两段四分之一圆弧的衔接处。
从点F的右侧看,螺线的曲率半径是EF,而从点F的左侧来看,点F处螺线的曲率半径却是HF。
HF<FE。
说明这条螺线的曲率在点F处是不连续的,虽然从图形中看不太出来。
实际的对数螺线是下图这样子的:
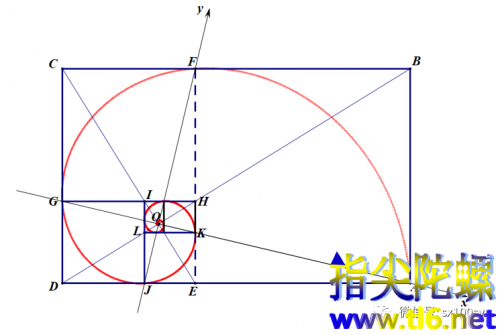
看上去与上一图没有什么区别(颜色不管)。
但若把两幅图叠加在一起,就可以看出细微的差别了。
如下图所示。
很显然,在点F的右侧,红色的真实螺线比蓝色圆弧稍微高一些,从而使得曲率稍微增加一点;而在点F的左侧,红色螺线比圆弧稍微低一点,从而曲率减少一点。
这样,在点F处的左右,螺线的曲率就连续了。
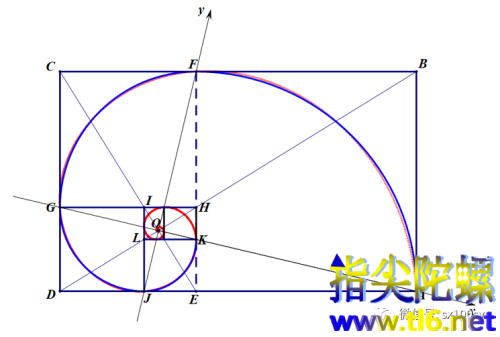
下面是对数螺线的生成过程。
那么,这个动画中对数螺线是怎么画出来的呢?注意观察上图及上面的动画,发现其中有直角坐标系Oxy。
再以点O为极点,以x轴为极轴,建立极坐标系。

黄金矩形中有很多很多的相似图形。
相似比就是黄金比0.618···。
从而,
FO:AO=0.618···
GO:FO=0.618···
JO:GO=0.618···
KO :JO = 0.618···
············
这就是说,把AO绕原点O逆时针旋转90°但长度减少到原长度的0.618···倍,得到FO;继续这一过程,依次得到GO,JO,···。
从而点A,F,G,J,K,···的极坐标可以用下面的函数表示(其中r为这些点到原点O的距离;不妨设AO=1,这不影响我们的研究,因为黄金矩形都是相似的,大小并不重要):

形式上,上式与直角坐标系下的指数函数一样。
回顾一下在直角坐标系下的指数函数:
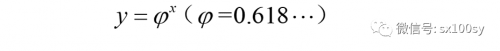
我们可以描绘出一些特殊的点,然后用光滑的曲线把它们连接起来,得到指数函数的大致图像。
如下图所示。
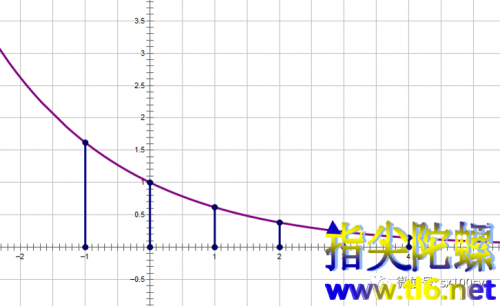
若自变量取一切实数,则指数函数就在定义域上是连续函数。
并且,指数函数的导函数也是连续的,即指数函数的切线是连续变化的。
那么,通过类比,我们也可以认为,在极坐标下,以函数

的极坐标描点,就是类似的特殊点,再用光滑的曲线把它们连接起来,得到一条同样处处连续且曲线的切线连续变化的曲线。
即下面的曲线:

这样一来,在点F处,就不存在曲率不连续的情况了。
在点G、J、K、···也一样。
观察一下发现,把“类扇形AOF”一边绕点O逆时针旋转90°,一边又在尺度上缩小到原来的0.618···,就转到了“类扇形FOG”的位置。
这就反映了对数螺线的自相似性。
一般用φ作指数函数的底很少见,我们一般是用常数e作底。
在高等数学中,对数螺线的极坐标方程是:
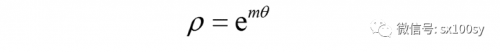
上式中“e”的前面“没有”系数,其实是系数为1。
这样的简化是合理的,因为ρ可以等于任意一个正实数。
于是我们就可以让极轴转动到经过(0,1)点。
对数螺线有一些奇特的性质,比如矢径与对数螺线的切线所成的角是一个常数(这就是对数螺线也叫做等角螺线的原因)。
再比如,由任意两条矢径与曲线的两个交点及极点可构成三角形,若两条矢径的夹角保持不变,则这样的三角形全都相似。
比如下图中的张角α=β,则三角形FOG与HOI相似(图中两三角形另一对对应角γ=δ)。
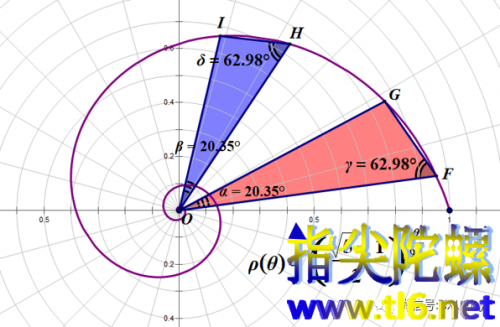
这第二条性质也是一种作对数螺线简单方法的基础。
在极轴上任取一点A,过点A作OA的垂线,再以O为顶点OA为一边作一个角,角的另一边与垂线交于点B。
以这种方式连续作出直角三角形AOB、BOC、COD、···。
其中∠AOB=∠BOC=∠COD=···。
然后把点A、B、C、D、···用光滑曲线连接起来,就得到对数螺线。
如下图所示。
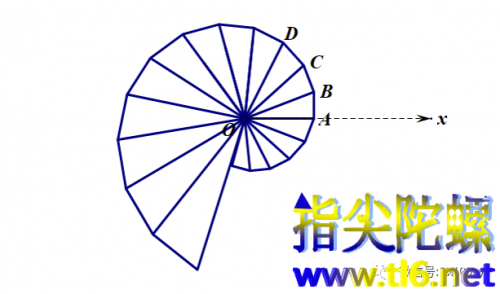
下面我们来确定对数螺线极坐标方程中的参数m,使得所得具体对数螺线正好是黄金矩形中所画对数螺线。
当θ=π/2时,ρ=φ。
所以,
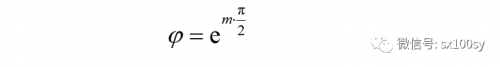
得出
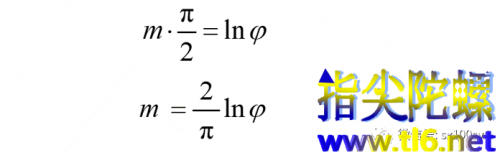
代入原方程,得
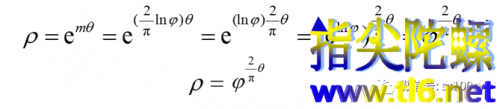
这就是黄金矩形中所画的对数螺线的方程。
显然,若自变量取等差数列:
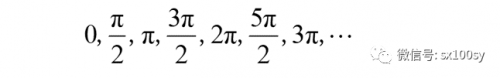
则函数值就是等比数列:
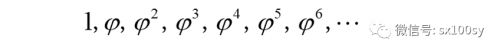
对应的点就是A,F,G,J,K,···。

用斐波那契数也可以生成“螺线”或“螺旋线”,但也只是与对数螺线接近,而不是真正的对数螺线(原因是,这里的矩形不是黄金矩形,只是越来越接近;不同圆弧之间的曲率也不连续)。
用斐波那契数生成“螺线”的过程大致如下图这样的:
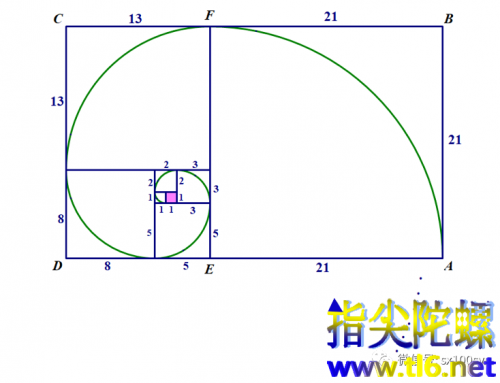
上图中从里向外的矩形及宽与长的比值分别是:
1×1矩形,宽:长=1:1=1>0.618···。
1×2矩形,宽:长=1:2=0.5<0.618···。
2×3矩形, 宽:长=2:3=0.6666···>0.618···。
3×5矩形, 宽:长=3:5=0.6<0.618···。
5×8矩形, 宽:长=5:8=0.625>0.618···。
8×13矩形, 宽:长=8:13=0.6153···<0.618···。
矩形DEFC, 宽:长=13:21=0.6190···>0.618···。
矩形ABCD, 宽:长=21:34=0.6176···<0.618···。
············
宽与长的比值与黄金数0.618···的差值的绝对值越来越小,极限矩形就是黄金矩形。
今天介绍了很多种“螺线”,只有对数螺线即等角螺线是最完美的。
本篇不涉及阿基米德螺线及双曲螺线。
它们是另两种不同螺线,以后陆续介绍。
最后,我们可以用软件画极坐标下的对数螺线。
上面讲螺线内部张角相等的三角形相似时,那幅图就是软件画的。

自变量用的是角度,所以,当θ=0时,ρ=1;当θ=90°时,ρ=0.618···;当θ=180°时,ρ=0.618···的平方≈0.382;当θ=270°时,ρ=0.618···的立方≈0.236。
从图中看,是很精确的。



















