相交圆法
如下图所示,点A和B位于一条直线上,点C位于点A和B之间,且离点B较近一些。我们要找到一点D,使得点C和D调和分割点A和B。
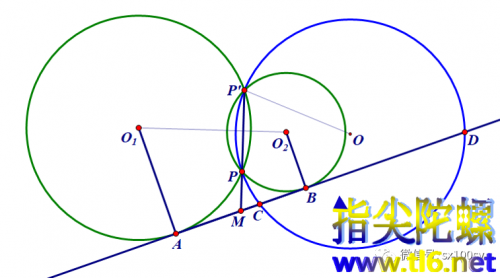
今天的方法姑且叫做相交圆法,因为我们将从下面作图中看到有两个相交的圆起到重要作用。如下图所示。分别过点A和B,在直线AB同侧作两条与直线AB垂直的线段AO₁和BO₂,并且要使两条垂线段一长一短,姑且让AO₁>BO₂。分别以点O₁和O₂为圆心作圆,让两圆相交(可以调整AO₁和BO₂的长度而做到)。得到两个交点P和P'。作一个过这两个点和点C的圆(过不在一条直线上的三点可以且只可以作一个圆,这里因为C离点B较近,所以C不是AB中点,而直线P'P必定过AB中点),即下图中的蓝色圆O。则圆O与直线AB除点C以外的另一个交点即为所求的两个调和分割点的第二个点(第一个点为C)。
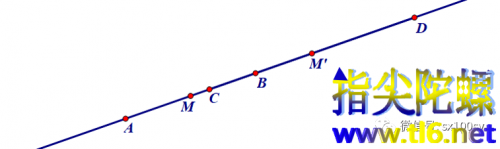
在证明前需先证明调和分割的一个性质和判定。如下图所示,点A和B被点C和D调和分割,当然点C和D也被点A和B调和分割,点M是AB的中点,点M'是CD的中点,那么,点M到点A和到点B的距离的乘积,等于点M到点C和到点D的距离的乘积,即MA·MB=MC·MD;点M'到点C和到点D的距离的乘积,等于点M'到点A和到点B的距离的乘积,即M'A·M'B=M'C·M'D。这个是调和分割的性质。反之亦成立,即判定。这个结论从上一讲所讲的反演出发不难得到。
下面证明本题的结论,即点C和D调和分割点A和B。如下图所示,MD是圆O的一条割线,MP'也是圆O的一条割线,所以,MC·MD=MP·MP'。MA是圆O₁的一条切线,MP'是圆O₁的一条割线,所以,MA²=MP·MP'。同理,MB²=MP·MP'。所以MA=MB。并且,
MA²=MB²=MA·MB=MP·MP'=MC·MD
所以,点A和B被点C和D调和分割,且点C和D也被点A和B调和分割。证毕。




















