
上一篇的探秘中提到,142857只是无数一七数中平平无奇的一个
实际上,一七数也只是众多“进制巧合”的一小部分。十进制系统的简洁对称,使得各种数学巧合层出不穷....(有机会再探讨更一般的进制)
此外,留言区提到了缺八数:
今天就通过一七数和缺八数,领略“进制的巧合”。
正题开始

一七数
定义
若p为素数,1/p的循环节长为p-1,则称循环节对应的数为一七数。

一七数的四个性质定理
轮转定理
翻车定理
拆和定理
平方拆和定理
通过四个定理可以很容易地构造性质数。
例如,用7进制数字构造与6相关的性质数:(0431162355)7
(0431162355)7×2=(1162355043)7
乘以1~10,得数均为0431162355的轮转
(04311)7+(62355)7=(66666)7
(14)7×(0431162355)7=(6666666666)7
(0431162355)27=(255620661133462644)7
(25562066)7+(1133462644)7=(1162355043)7
一七数除了上述四个特性,还有很多,以142857为例。
142857×8=1 14285 6142857×9=1 28561 3...142857×13=1 85714 1
这是词条上的例子。
把得数的“头”加到尾巴上,又得到142857的轮转数。基本原理
以乘8为例:

于是“头部添1,尾部减1”,上边性质就出现了。
延伸|一七数有多少?
如果考虑不同进制,一七数可以有无穷多个。
1/7的循环节在3,10,17,24,...等3+7k进制中,长度均为6,因而都构成一七数。
如果考虑特定进制,就不好说了。
容易证明,平方进制4,9,16...中不存在一七数。
统计显示:
3-10000的进制中,除平方进制外,都含有一七数。
在十进制中,也有大量一七数,5w以内有1947个素数可生成一七数。
猜想
若m进制中含有一七数,则必含无穷多的一七数。
缺八数

缺八数指12345679。这里讨论它的2个性质。
一、乘九归一
12345679×9=111111111
二、乘八倒序
12345679×8=98765432
原理解释
性质一
先考虑123456789与9的乘积

产生一排1的原因在于错位相减。

通过“不缺数”123456789作媒介,论证缺八数的性质。
性质二
考虑123456789+987654321=
1111111110
加1减1:

性质二也有了。
由于讨论过程不依赖所处进制,一般地,m进制下“缺m-2数”都有上边性质。
9进制下1234568×8=1111111
1234568×7=8765432
8进制下123457×7=111111
123457×6=765432
数学探究没有终止线,一个问题的结束往往伴随更多新问题的产生。
性质推广
一、推广缺项
把其他缺项数乘2
23456789×2=46913578(缺2)
13456789×2=26913578(缺4)
12456789×2=24913578(缺6)
12356789×2=24713578(69→7)
12346789×2=24693578(缺1)
12345789×2=24691578(缺3)
12345689×2=24691378(缺5)
12345679×2=24691358(缺7)
12345678×2=24691356(78→6)
右边得数均和246913578紧密相关
考虑不缺数乘2
123456789×2=246913578
得数便为246913578
巧合太多,不免疑惑:随便玩都有这些“巧合”吗?交换3和4的位置试试。
124356789×2=248713578
数字7和8重复了
数的次序不能交换,也说明次序是性质产生的关键
二、推广进制
进一步看,这些性质与所处进制密切相关偶数进制下乘28进制:1234567×2=2471356
6进制:12345×2=25134
得数都是不缺数
奇数进制下乘2,9进制:12345678×2=24702467
7进制:123456×2=250245
得数都有重复数字。
三、推广乘数
乘一般的数又会怎样?
一般地,弄懂十进制,其他进制也会一并迎刃而解。
这里抛一块砖,感兴趣不妨顺着思路走下去,动手摸索往往有更多惊喜和乐趣。
对于123456789
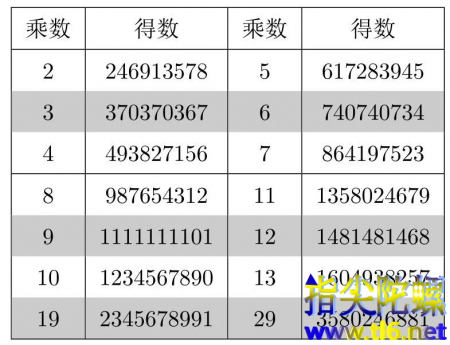
表格中,白色栏的得数都是不缺数,灰色栏得数都出现了重复数字。容易发现,当乘数被3整除或尾数为9时,得数出现重复数字。。。
总结导图
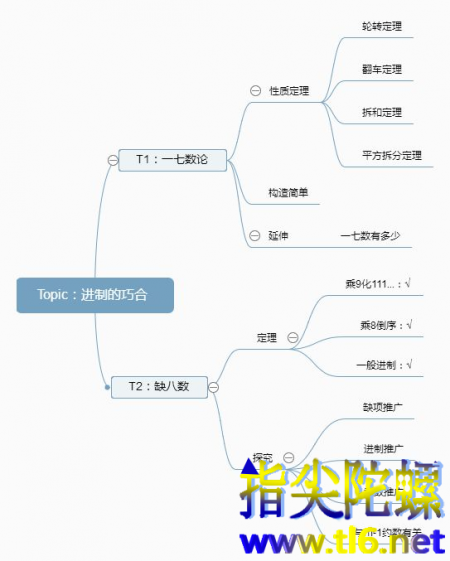
进制的巧合还有很多很多,一七数和缺八数只是其中两例。正是这些巧合的存在,数学才越加好玩。



















