平方数与质因数的指数
上传时间：2020-11-27 09:10点击:
一个自然数平方后，得到的数叫做平方数，或者完全平方数。比如：
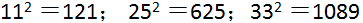
这里的121、625、1089就是平方数，我们把平方数分解质因数以后观察一下：
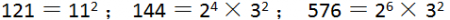
我们可以观察出来，各质因数的指数都是偶数，所以有以下结论：
结论
一个平方数分解质因数以后，各质因数的指数都是偶数；
反之，如果一个数分解质因数以后，各质因数的指数都是偶数，那么这个数一定是完全平方数。
这个结论有什么用呢？利用上面的结论，我们可以做下面的题目。
例29645是平方数吗？
我们首先将29645分解质因数，得到：
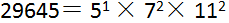
很明显，其中一个质因数5的指数是奇数，所以这个数不可能是平方数。
例
一个整数与1080的乘积是一个完全平方数，那么这个整数最小是几？
我们首先将1080分解质因数，得到：
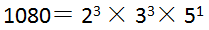
要达到完全平方数，需要使得各个质因数上的指数为偶数，所以我们需要补足，需要乘以指数为奇数的质因数，也就是：
2×3×5＝30
这个整数最小应该为30，当然，更大的只要继续乘以2、3、5的偶数次方即可。
