什么是最大公约数?
基本概念
最大公约数:几个数公有的约数,叫做这几个数的公约数,其中最大的,就叫做最大公约数;
互质数:如果两个数的最大公约数是1,那么这两个数叫做互质数
最大公约数的求法有很多种,常见的有质因数分解法、短除法、辗转相除法、更相减损法,需要根据情况灵活运用。
1质因数分解法
质因数分解法就是将这几个数分解质因数,找出他们共同都有的质因数进行连乘,就得到最大公约数。
例:求42和140的最大公约数
84=2×2×3×7
140=2×2×5×7
2×2×7=28
所以42和140的最大公约数是28
2
短除法
短除法就是先用这几个数的公约数连续去除,一直除到所有的商互质为止,然后把所有的除数连乘起来,所得的积就是这几个数的最大公约数。
例:求30、60和75的最大公约数
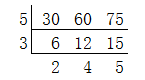
3×5=15
所以30、60和75的最大公约数是15
3
辗转相除法
辗转相除法是把这2个数的较小数去除较大数,得到的余数去除之前的除数,依次进行,直到余数为0为止,最后一次的除数就是他们的最大公约数。
多个数怎么办?可以两两求出最大公约数,再用不同的最大公约数相互两两求,直到最终结果。
这个方法非常适合无法做质因数分解(一下子看不出质因子)的时候快速使用。
例:求2703和1113的最大公约数
2703÷1113=2……477
1113÷477=2……159
477÷159=3
所以2703和1113的最大公约数是159
4
更相减损法
更相减损法也叫等值算法,先判断两个数是否都是偶数,如果是,用2约分至不是同偶。
然后用较大数减去较小数,把得到的结果与之前的减数继续比较,依次操作,直到结果为0为止。
同碾转相除法的本质是一样,只不过用相减替代了求余,步骤会更多,一样适用于任何需要求最大公约数的场合。
例:求2703和1113的最大公约数
2703-1113=1590
1590-1113=477
1113-477=636
636-477=159
477-159=318
318-159=159
159-159=0
所以2703和1113的最大公约数是159



















