最大公约数的应用
上传时间：2020-12-18 20:46点击:
只是求几个数的最大公约数，上次已经教过几种不同的方法，但是如何从一个应用题想到去求最大公约数，需要更多的训练。
1一张长方形的纸，长2703厘米、宽1113厘米，如果把这张纸裁成若干个同样大小的正方形，纸张不允许有剩余，需要恰好使用完，那么这样的正方形最大边长是多少厘米？
这个题目的实质是，要求出一个最大的边长，使得从长的方向来说正好裁剪完若干个这样的边长，宽的方向也是。这就是说，要求出一个2703和1113的最大公约数。
用辗转相除法来做：
2703÷1113＝2……477
1113÷477＝2……159
477÷159＝3
所以2703和1113的最大公约数是159
也就是说，这样的正方形最大边长是159厘米。
2
将一个长25厘米、宽20厘米、高15厘米的长方体分割成完全一样大小的正方体，且不能有剩余，那么这个正方体最大的边长是多少？
同上题类似，本质是求25、20、15的最大公约数，这道题很简单，最大公约数是5，所以这个正方体最大边长就应该是5厘米。
3
已知两个数的积是5766，它们的最大公约数是31，那么这两个数是？（难度★★★☆）
还记得上一个讲的短除法吗？比如求30、60和75的最大公约数
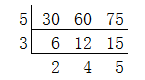
3×5＝15，所以30、60和75的最大公约数是15。也就是说，用15乘以余下的3个数，可以分别得到20、60、75，也就是说，余下的2、4、5相乘，然后乘以3个最大公约数，就可以得到这3个数的乘积。
回到原题，假设这两个数除以31的余数分别是A和B，那么：
A×B×31×31＝5766
A×B＝6
由于6＝1×6＝2×3
所以原来的2个数字可能是1×31和2×3×31，或是2×31和3×31，也就是31和186，或者是62和93
