直线相交，多少交点？
上传时间：2020-12-22 21:37点击:
这是个有意思的问题，两条直线相交，多少个交点？那肯定只有一个对不对？十条直线呢？当然最少也只有一个，只要这十条穿过一个点相交即可，比如：
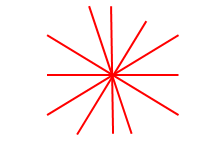
可见，求最少交点没太大意义，所以我们一般是求最多有多少个交点。我们现在已经知道：
①一条直线，最多0个交点；
②两条直线相交，最多1个交点；
③三条直线相交，最多3个交点；
④四条直线相交，最多6个交点；
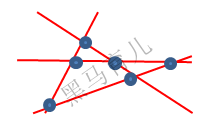
⑤五条直线相交，最多10个交点；
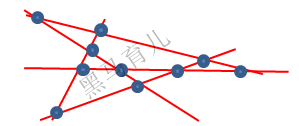
我们先来看看0、1、3、6、10，这是不是有点眼熟？不熟也没关系，我们只要看看《找规律·找数字规律（二）：搭桥法介绍》，就能看出来，下一个数字应该是在此前10的基础上加5，等于15，也就是说，如果按此规律：
六条直线相交应该最多15个交点；
七条直线相交最多21个交点；
八条直线相交最多28个交点；
九条直线相交最多36个交点；
十条直线相交最多45个交点。
那么这个规律是否存在呢？我们用九条直线来验证一下：
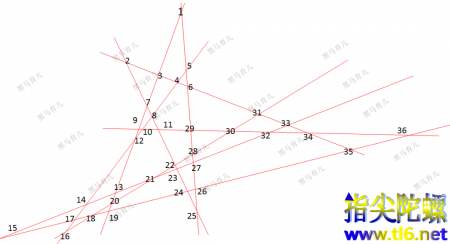
九条直线最多确实是36个交点。
所以我们归纳总结出来的结论就是：
N条直线，最多有从1加到（N－1）个交点。
正如上面验证的，N＝9的时候，交点数最多是从1加到8，也就是36个。
