其实更好玩的题目是切西瓜,不过太立体了,对于二年级的来说,先来玩玩直线分圆,或者说是刀切圆饼。跟直线相交一样,如果每刀交点都在一起,那么每一刀都会增加2块,2刀4块、3刀6块、4刀8块,比如:
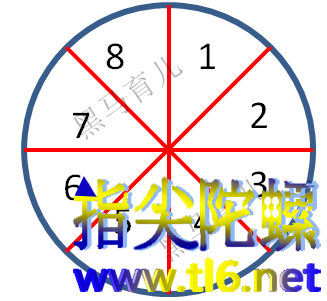
跟直线交点一样,我们一般是求一刀切下去,最多能分成多少块。我们现在试试:

可以看到:
①0条直线,最多分成1块(还是那个圆);
②1条直线,最多分成2块;
③2条直线,最多分成4块;
④3条直线,最多分成7块;
⑤4条直线,最多分成11块。
现在我们来看看这个数列的规律:1、2、4、7、11,通过搭桥法,我们很容易发现,后面一个数与前面一个数之差,是一个自然数列,所以我们列出对应关系:
0条直线最多分成1=1块;
1条直线最多分成1+1=2块;
2条直线最多分成1+1+2=4块;
3条直线最多分成1+1+2+3=7块;
4条直线最多分成1+1+2+3+4=11块;
我们猜测一下吧,按这个规律来说,如果N=6,最多可以分成:
1+(1+2+3+4+5+6)=22块
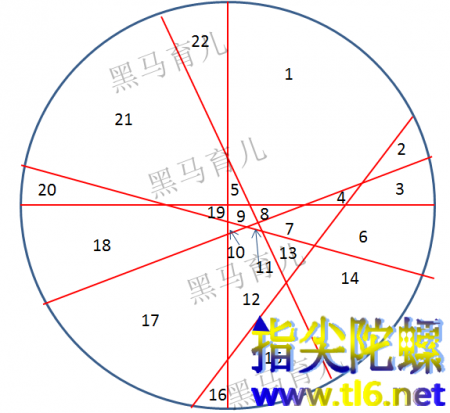
切了好几次,总算切出来确实是22个,所以,以上推论确实成立的。
那么,我们归纳总结一下规律:
N条直线去切分圆,最多能分成1+(1+2+…+N)块。



















