简单幻方的解法口诀
上传时间：2020-12-31 09:25点击:
关于幻方，我们在《【四年级】认识幻方》中已经介绍过，这里就不重复说了，今天主要是介绍一下古人对三阶幻方的一种巧妙做法。
古代对三阶幻方又叫做九宫，我国南宋著名数学家杨辉曾对之进行过精心研究。在他所著的《续古摘奇算法》中，列出了一种十分巧妙的解法，其口诀是：
九子斜排，上下对易，左右相更，四维挺出
这句话的意思是，把1-9这9个数，按照由小到大的顺序排列，然后，以3个数为一排，斜着排列；后续3个数作为第二排，也斜着排列；最后3个数作为第三排斜着排列。
然后，将这一个菱形数阵图的上下2个数字位置对调、左右2个数字位置对调。
最后，将4条边上中间的数向外挺出，将菱形变形成正方形，就可以了。
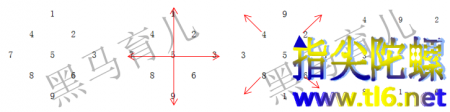
动画展示一下：
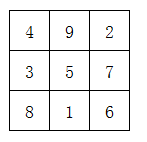
最终的结果：
那么，四阶幻方有没有类似于三阶幻方的口诀呢？很幸运，也有：
一字排开，对角不动，上下交换，左右更替
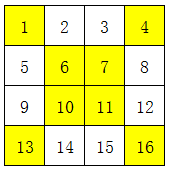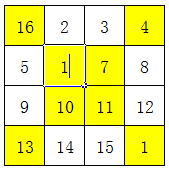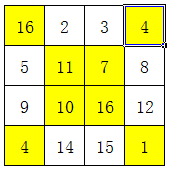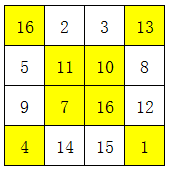
这句话的意思是，把这16个数，按照由小到大的顺序排列，然后，以4个数为一排排列；依次完成第2~4行。
然后，将这一个4×4方格中，凡是不在对角线的数字，按照上下互换、左右互换的方式调整。
最终得到的就是四阶幻方了，解题过程如下图，其中黄色部分是对角线上的数字，锁定不动：
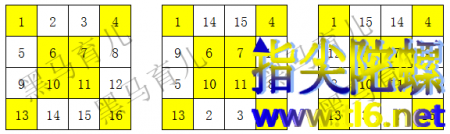
动图如下：
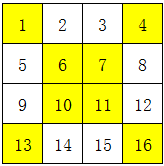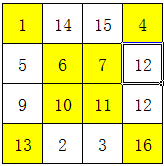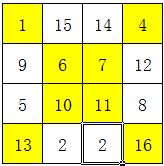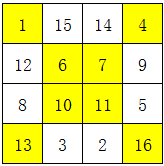
对于四阶幻方，其实还有个做法：
一字排开，对角互换
这个做法跟上述做法恰恰相反，只动对角线上对称的数字，互换位置即可。
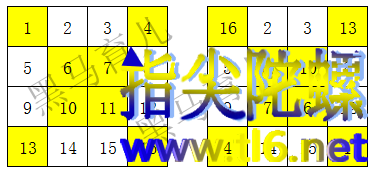
动图如下：
