这是一个有趣的问题，它曾经是一道竞赛题，但标准答案却是错误的。一位小考生指出了错误，评委不得不改判这位考生正确。具体来说，题目是：有一个正四棱锥（底面为正方形的直棱锥），四个侧面都是正三角形；另有一个正四面体，它的三角形面与正四棱锥的侧面一样大小。若把这两个立体在某个正三角形面处完全重合地粘贴在一起，问组合体有多少个面？

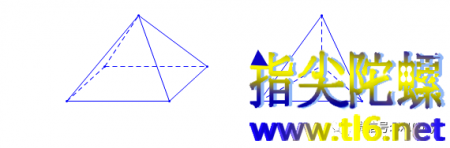
一般的考生及标准答案都是这样思考的：正四棱锥有5个面，正四面体有4个面，组合后，各有一个正三角形面被互相盖住而消失，从而组合体有5+4-2=7个面。

那位考生发现，并非如此。我下面用图说明错误错在哪里。

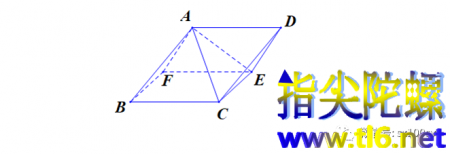
如上图所示，看似三角形面ABC与ACD面有共用边AC。于是，一般都会认为ABC和ACD是两个面。但其实，它们位于同一个平面上。同理，AFE与ADE也位于同一个平面上。所以，实际上，组合体就只有5个面：三角形面ABF和CDE，平行四边形面ABCD和AFED，正方形面BCEF。

那么，这什么三角形ABC面与三角形ACD面位于同一个平面上呢？这个不难回答。我今天提出这个问题，也是为了后面新知识的讲解。

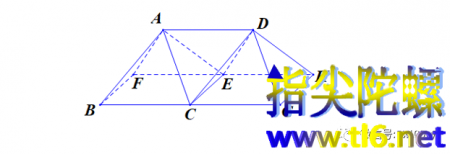
我们不妨把两个上面那种侧面是正三角形的正四棱锥并排放置，如下图所示中的A-BCEF和D-CGHE。那么一下子就可以看出上面问题的本质所在。ABC与CDG是互相平移而得来的，当然在一个平面上，并且AC=CD=AD=CE=AE=DE。所以，ACDE是正四面体。三角形ACD一定与ABC和CDG位于同一个平面上，没有问题的。

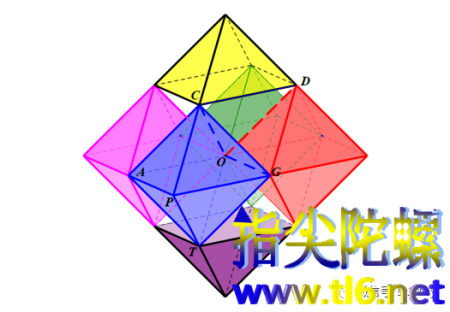
上面的问题就算回答清楚了。下面我们进行拓展。把四个这样的正四棱锥排列成“田”字形。如下图所示。（换了个角度，加了颜色，所以更加好看。像四座金字塔。）

那么，从上图可以看出，每两个并列的正四棱锥之间都可以“夹着”一个正四面体。共四个这样的正四面体（如下图中的OACF、OGDC、OBED、OHFE）。也就是说，把这四个正四面体补上后，四座山就变成了座“环形山”（山上出平湖的山都大致是环形山，把水围住流不出来）。若把这个“环形山”注满水，则这个水体的形状就是一个倒置的正四棱锥：O-CDEF。如下图所示。

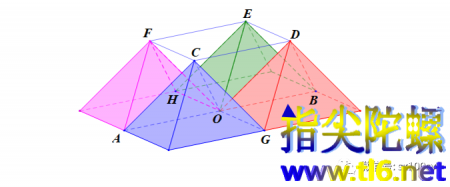
在正方形CDEF上面再摞一个正四棱锥，我们就得到一个大四棱锥，如下图的K-PQRS。这个大四棱锥与原四棱锥相似，尺度大了一倍。（为了看得清楚，那四个正四面体是空着的，倒置的正四棱锥也是镂空的，所以，看上去这个大正四棱锥就好像是灰色正四棱锥的四个下角点搭在了下面四个正四棱锥的顶峰上。）

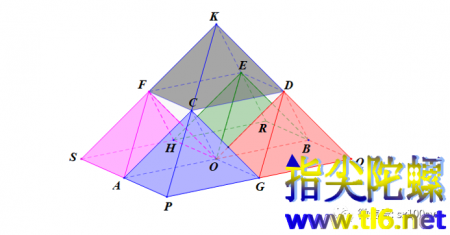
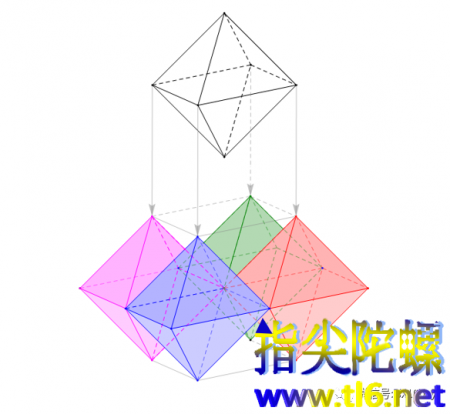
我们还知道，一个正八面体是由两个上述正四棱锥在底面对接在一起得到的。所以，上图中的K-CDEF-O就是一个正八面体。所以可以这样看待大正棱锥的构成：在四座正四棱锥山峰之间从上向下插入一个正八面体。如下图所示。

然后再用四个正四面体从四个侧面把“山谷”塞住。于是就真正得到了一个大的正四棱锥（K-PQRS）。

若把平面PQRS当成水平面，PQRS的外围都是水，则我们从远处可以看到大正四棱锥的倒影。原影与倒影合在一起是一个大的正八面体。如下图所示。

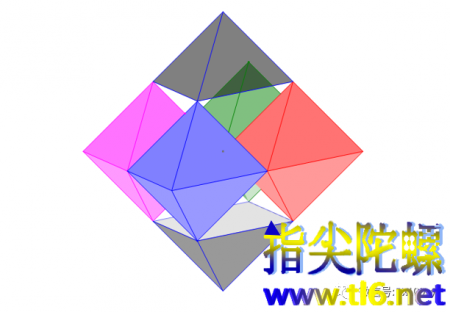
由此可以看出，一个正八面体可以分解成六个尺度减半的小正八面体（正八面体有六个顶点，所以小正八面体是六个）。每两个小正八面体之间有两个正四面体，12×2÷3=8，所以一共有八个正四面体（与正八面体有八个面相对应）。

下面再简单介绍一下用正八面体和正四面体如何密铺整个空间。来看一下这幅图：

把APGO-FCDE单独取出来，如下图所示。它是一个平行六面体，由两个正四棱锥C-APGO和O-FCDE及两个正四面体OACF和OGDC构成。也可以说由被分成两半的一个正八面体和两个正四面体构成。

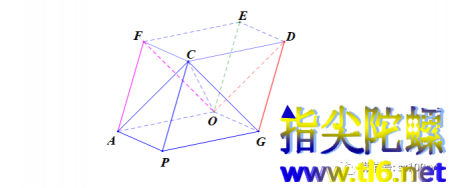
我们知道，平行六面体通过复制自身并沿着不同三条边的方向平移，可以充满整个空间。我们对这个平行六面体进行这样的操作时，将会得到一层层的正八面体。可以打个比较形象的比喻：我们购买的有托盘的整盒鸡蛋。

就这样充满整个空间的正八面体和正四面体的个数之比为1:2（从前面的平行六面体可以得知）。但由于一个正八面体的体积是一个正四面体的体积的4倍，所以，整个空间中正八面体与正四面体的体积之比是2:1。

再来看一看这种密铺中，每个顶点、边、面、体周周的情况如何。每个点（比如点O）都连接着6个正八面体和8个正四面体，并且互相交叉着。每条边（比如OG边）都连接着2个正八面体和2个正四面体，也是互相交叉着。每个面（比如OCG）都连接着1个正八面体和1个正四面体（即一个面两侧一定是不同类似的正多面体）。八个正四面体围着一个正八面体（这个很好理解，因为一个正八面体有八个正三角形面，这八个正三角形面外接着的一定是正四面体，上一句话已解释）。四个正八面体之间围着一个正四面体（比如考虑下图中蓝色、红色、黄色（下半截没有标黄）三个正八面体，在三角形CDG外侧贴放一个正八面体，所以这里所说的“四个正八面体围着一个正四面体”中的“四个正八面体”是这样的一种摆放方式，它们围着的正四面体是OGDC）。