奇数阶幻方解法
上传时间：2021-01-03 16:53点击:
奇数阶幻方最经典的填法是罗伯特法，也有另外一个比较通俗的叫法——楼梯法。该方法为：
1.把这一系列数中按照从小到大的次序排列，然后将第一个数（最小的数）放在第一行的中间，剩余每一个数都放在前一个数的右上一格；
2.如果这个数要放的格已经超过了顶行，那就把它放到底行，但仍然要放到右一列；
3.如果这个数要放的格已经超过了最右列，那么就把它放在最左列，但仍然要放到上一行；
4.如果这个数要放的格已经超过了顶行且超过了最右列，那就把它放到前一个数的下一行的同一列的格中；
5.如果这个数要放的格已经有数字填入，则重复第4步；
这种方法主要是向右上爬，很像是在爬楼梯。
我们以一个五阶幻方为例，填入9-33这25个数
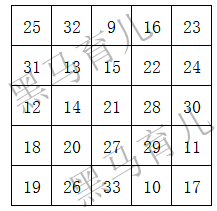
右图是最终结果，我们检验一下：每行、每列、对角线之和都是105，也就是说这个幻方的幻和是105
我们四年级学过“九子斜排，上下对易，左右相更，四维挺出”口诀解决三阶幻方问题，如果用楼梯法其实更快。
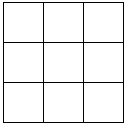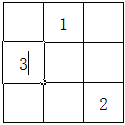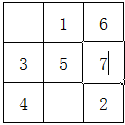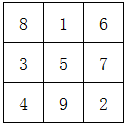
再来试一下七阶幻方，看看做一下是不是也很快：
