所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方,即4K阶幻方。在说解法之前我们先说明一个“互补数”定义:就是在n阶幻方中,如果两个数的和等于幻方中最大的数与最小数的和(即n×n+1),我们称它们为一对互补数。如在1~9的三阶幻方中,每一对和为10的数,是一对互补数;在1~16的四阶幻方中,每一对和为17的数,是一对互补数。
回忆一下四年级学习过的四阶幻方的解法《【四年级】简单幻方的解法口诀》,当时是使用了“一字排开、对角互换”的方法:
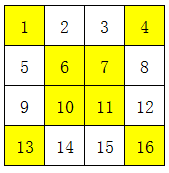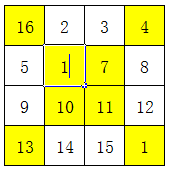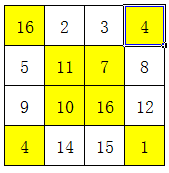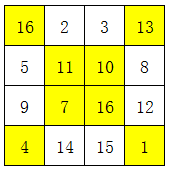
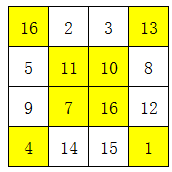
其实所谓的对角互换,应该理解为对角线上的数,都换成自己的补数。
那么,双偶数阶幻方的解法是什么呢?对称交换解法。具体来说,就是把数字从小到大按顺序填写到4k×4k的方阵中,然后:
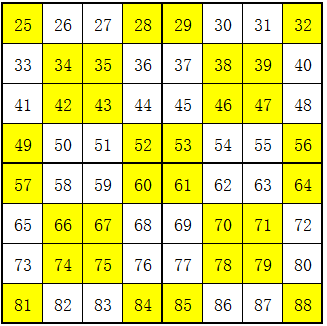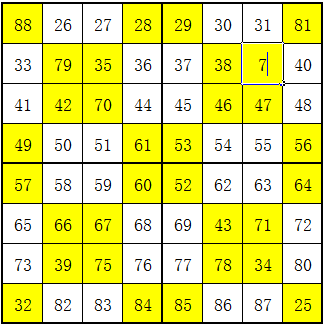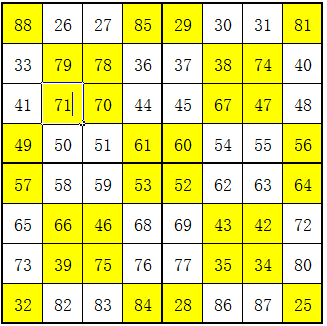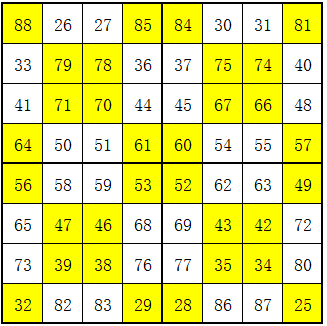
按4×4把它划分成k×k个方阵。因为n是4的倍数,一定能用4×4的小方阵分割。然后把每个小方阵的对角线,象制作4阶幻方的方法一样,对角线上的数字换成互补的数字,就构成幻方。
我们来试试一个八阶幻方,这个幻方是从25~88总共66个数,总和为113的数互补,解题过程如下图:
最终结果

幻和确实是:
(25+88)×64÷2÷8=113×4=452



















