今天介绍二次曲面，但我想从直观上进行讲解。

一个圆，沿着与圆所在平面垂直的方向平移，轨迹是一个圆柱面。类似地，把圆换成椭圆、抛物线或双曲线，作同样的平移，轨迹将是椭圆柱面、抛物柱面或双曲柱面。

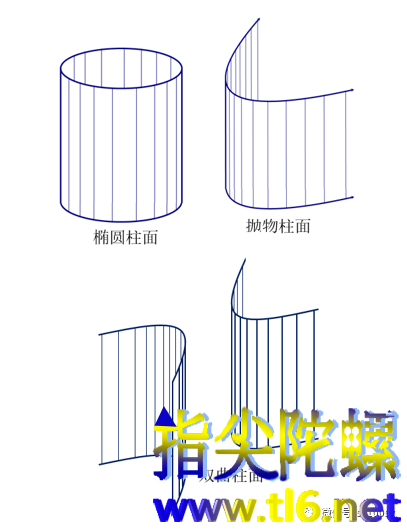
椭圆柱面、抛物柱面或双曲柱面也可以理解为一条过椭圆、抛物线或双曲线且与其所在平面垂直的直线（母线）沿着曲线运动所产生的轨迹。

空间中一条直线绕与其平行的另一条直线旋转一周，形成的曲面为圆柱面。空间中一条直线绕与其相交的另一条直线旋转一周，形成的曲面为圆锥面。那么，空间中一条直线绕一条与其异面的直线旋转一周，形成的是什么曲面呢？是旋转单叶双曲面。我后面将会仔细介绍。（我们在科技馆中看到的那个演示——一条绕轴旋转的直棒竟然可以穿过“双曲线缝隙”——就是利用了旋转单叶双曲面的知识。科技馆中的实验起到了培养和提升中小学生学习数学和科学的兴趣，功不可没）。

空间中直线可以绕轴旋转形成曲面，那么空间中的椭圆、抛物线、双曲线沿着各自的对称轴旋转将形成什么曲面呢？椭圆有两个互相垂直的对称轴，若绕长轴旋转半周，将形成一个类似鸡蛋壳的旋转椭球面；若绕短轴旋转半周，则形成类似地球表面的旋转椭球面（可能是因为地球自转的原因，离心力使得地球不是一个纯粹的圆球，而是有些“扁”的椭球）。旋转椭球面在两个维度上是相同的，第三个维度不同。抛物线有一个对称轴，抛物线绕这个唯一对称轴旋转半周，所得为一个叫做旋转抛物面的二次曲面。双曲线有两个对称轴，一个是实轴，一个是虚轴，双曲线绕实轴旋转半周，将形成旋转双叶双曲面；双曲线绕虚轴旋转半周，将形成旋转单叶双曲面。

上面所讲包括下面这些曲面：

①圆柱面，②圆锥面，③ 椭圆柱面，④ 抛物柱面，⑤ 双曲柱面，⑥旋转椭球面，⑦ 旋转抛物面，⑧旋转双叶双曲面，⑨旋转单叶双曲面。

上面这九种远不是二次曲面的分类，有很多是可以推广到更一般的情况，并且还有遗漏（我们后面会补充上的）。为了推广，我们需要先了解下面这个概念，即所谓的“伸缩变形法”，也称作“向着一条直线的伸缩”（可以与“向着一点的伸缩”对比）。所谓伸缩变形是指把一条平面曲线上所有点向着与同平面上一条直线垂直的方向同时伸缩相同的比例。举个例子，把一个圆的所有点向着与一条直径垂直的方向伸缩1/2，将得到一个椭圆，如下图所示。

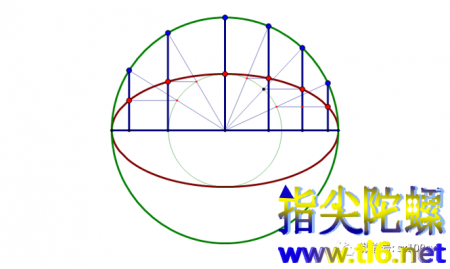
把在平面上向着直线的伸缩变换拓展到空间中就是向着平面的伸缩变换。

那么，把前面①号圆柱面沿着与轴垂直的某一方向进行伸缩变换，就将得到椭圆柱面，即上面的③号。把②号圆锥面沿着与轴垂直的某一方向也进行这种伸缩变换，将得到二阶锥面或椭圆锥面。把⑥号旋转椭球面沿着与旋转轴垂直的某一方向进行伸缩变换，将得到一般的椭球面。一般的椭球面只有三个对称面，而旋转椭球面有无数多对称面（过旋转轴的平面都是对称面）。把⑦号旋转抛物面作类似的伸缩变换，将得到椭圆抛物面。对⑧号旋转双叶双曲面和⑨号旋转单叶双曲面也分别实施这种伸缩变换，将分别得到一般的双叶双曲面和单叶双曲面。

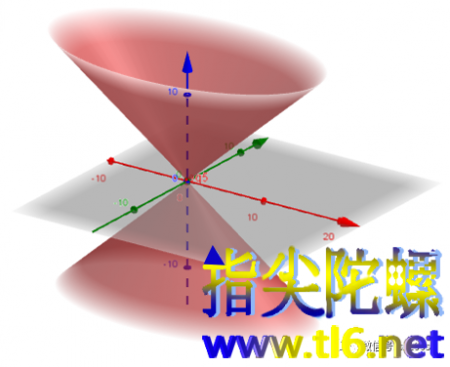
二阶锥面

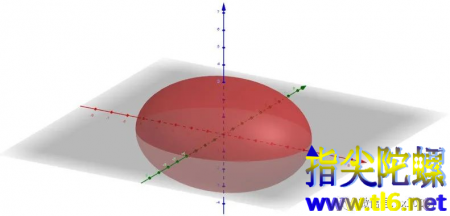
椭球面

椭圆抛物面

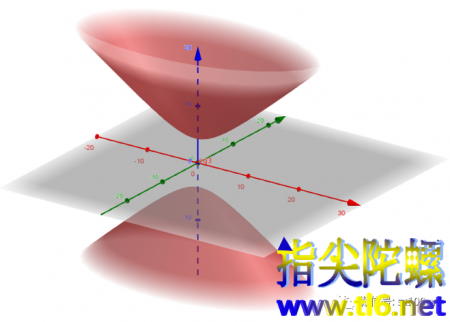
双叶双曲面

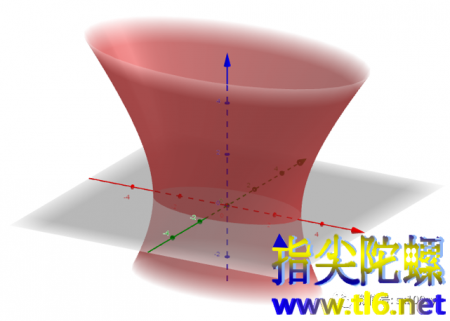
单叶双曲面

我们现在得到了八种二次曲面：(1)椭圆柱面，(2)二阶锥面，(3)抛物柱面，(4)双曲柱面，(5)椭球面，(6)椭圆抛物面，(7)双叶双曲面，(8)单叶双曲面。还有一种，不能通过上述的方法获得，那就是所谓的“马鞍面”，正式名称叫做双曲抛物面(9)。所以，一共是九种二次曲面。

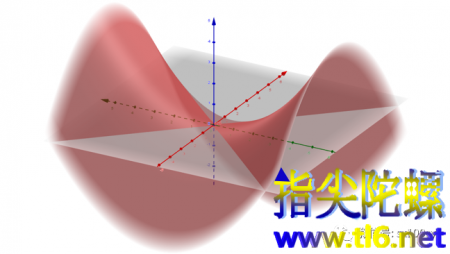
双曲抛物面

这九种二次曲面中，有六种是所谓的直纹面：椭圆柱面，二阶锥面，抛物柱面，双曲柱面，单叶双曲面和双曲抛物面。前四种都可以将其沿一条直纹（母线）剪开而铺展到一个平面上，而单叶双曲面和双曲抛物面则不能。所以它们有些特别。单叶双曲面可以通过空间中两两异面且不都平行于同一平面的三条直线生成（注意，三条直线虽然可以做到两两都是异面直线，但不能避免三条直线都与同一平面平行）。这样的三条直线在下面将被称作处于一般位置关系。这个很有趣，我们今天稍微详细地讲解这种生成单叶双曲面的方法。

在空间中任取三条处于一般位置关系的直线。与这三条直线都相交的直线将有无数多条。理由是：我们可以过其中一条直线作一个平面，并让这个平面绕这条直线旋转。这个平面只可能存在两个位置它不与另两条直线都相交（在其中一个位置，它不与第二条直线相交，在另一个位置时它不与第三条直线相交），而在平面旋转到的其他所有位置处，平面与第二条和第三条直线都相交。过这两个交点的直线除个别情况外，都与第一条直线相交。这就是说，存在无数条直线，它们与已知的三条处于一般关系的直线都相交。

到此我们要引出的结论是：无数多条这样的直线不多不少正好可以生成一个单叶双曲面。真是很神奇！注意，旋转单叶双曲面只是一种特殊情况，是一种比较好理解的情况。其实，选取任意三条处于一般关系的直线，则与它们都相交的直线都将生成单叶双曲面。

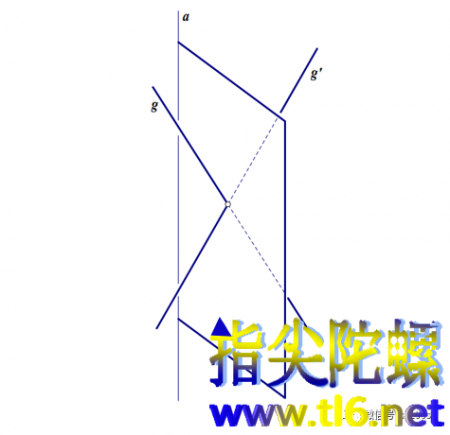
单叶双曲面有两族直线，每一族都可以单独生成单叶双曲面。一族中任意一条直线都与另一族中的每一条曲线相交或平行，但同一族中任意两条直线都是异面的（或说都是敧斜的）。单叶双曲面上任意一点都是某一族直线中的一条与另一族直线中的一条的交点，这两条直线是关于过交点也过旋转轴的平面对称的。如下图所示。直线g绕轴a旋转一周后形成旋转单叶双曲面，而直线g'绕轴a旋转一周同样可以形成同一单叶双曲面。这个从直观上看也很显然。

下图是旋转单叶双曲面的一部分，只是示意，像个篮球网。

双曲抛物面也是直纹面，但它与单叶双曲面的生成是不同的，即不能通过绕固定轴旋转直线得到。双曲抛物面也是有两族直线，每一族也都可以单独生成双曲抛物面，但同一族中的所有直线虽然互相都异面，但却都平行于某一个平面。这是与单叶双曲面的重要不同之处。可以观察下图，我们找到那个水平的虚线平行四边形（其实是矩形）从左上到右下的那条对角线，它与z轴构成一个平面，然后，左侧和下侧“马鞍面”中“\”方向的直纹都与这个平面平行，但与平面的距离不同，且逐渐向一个方向扭转。是不是这样的？直观上是这样的，若想从理论上理解，需要用到它的标准方程来研究。

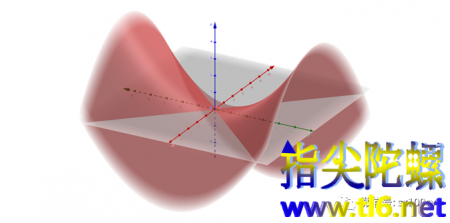
还希望读到这里的你有能力用GeoGebra软件画出一族直纹，然后让“马鞍面”转动位置以观察这组直纹之间的关系及与那个与它们都平行的平面的关系。

参考书：

[1]《解析几何》（吴光磊 丁石孙 姜伯驹 田 畴 编）人民教育出版社

[2]《直观几何》（D.希尔伯特 S.康福森 著  王联芳 译）高等教育出版社