傅立叶变换
今天，先放个动图给大家猜猜今天文章的主题（不要偷看哦。。。）
巴拉拉，变身吧！！！
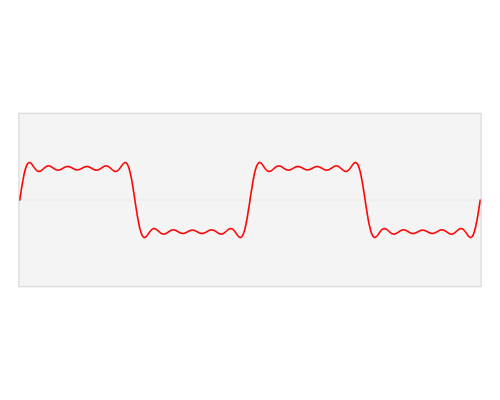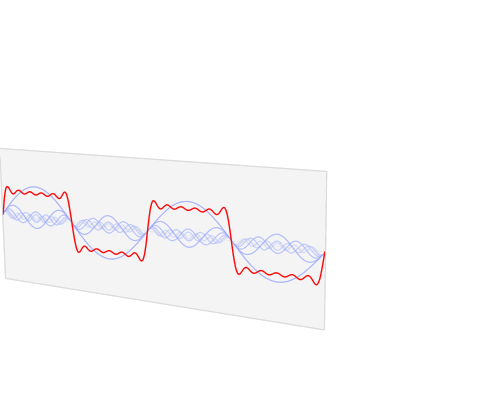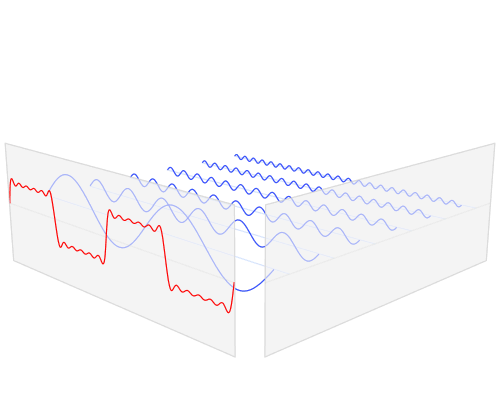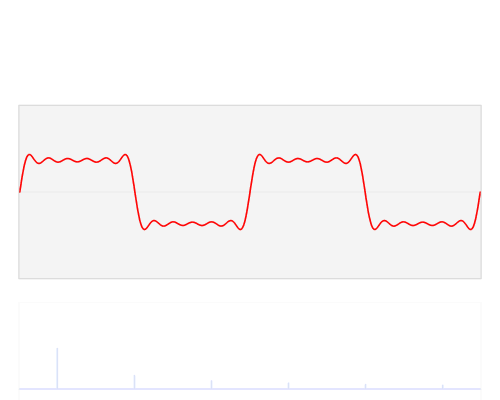
图片作者：LucasVB
突然发现自己的小心思被标题给出卖了（小天，你这标题起的真好。。。）
言归正传，超模君今天要跟大家分享的确实是工科大神器——傅立叶变换。
说到傅立叶变换，就要先讲讲傅立叶：
（1768~1830）
傅立叶出生于法国，是一名浪漫的法国数学家，同时也是一名视角独特的数学家。
而他的独特是因为：他不像其他科学家那般死抓着纯数学研究，而是致力于将数学应用于实际生产。
而这种理念与当时纯数学研究为上总有点格格不入，幸运的地是傅立叶遇到拿破仑，一个超级热爱科学的皇帝（如果他没有成为将军，那他将会是下一个牛顿）。此后，1798年傅立叶就随拿破仑军队远征埃及，受到拿破仑器重，回国后被任命为格伦诺布尔省省长。
回国后的傅立叶，除了处理行政工作，也从未放下学术研究。
1811年，傅立叶向科学院提交二次修改过后的文章《热的传播》，该篇文章也为傅立叶获得了科学院大奖。
傅立叶在论文中推导出著名的热传导方程 ，并提出了傅立叶变换的基本思想。
也就因为这个基本思想，直接造福工程界、数学界。
甚至在数学界、工程界有这么一句传说：
有一种运算，把微积分变成加减乘除，它叫傅立叶变换。
那傅立叶变化到底怎么解决问题的呢？
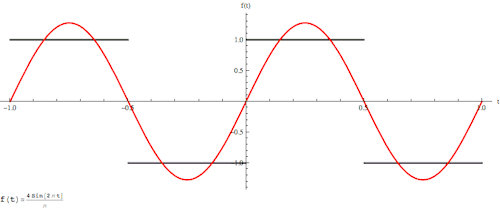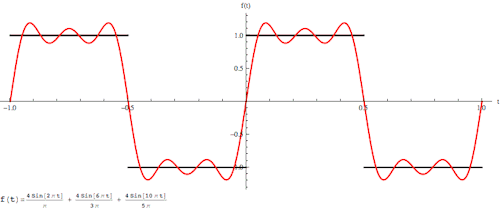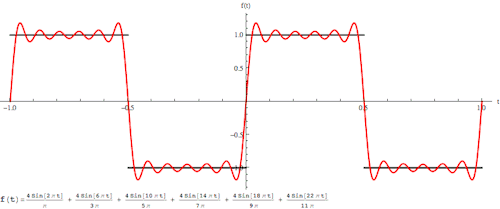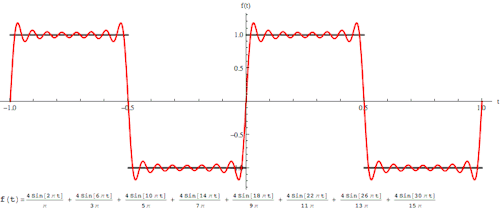
其实，傅立叶变换（的三角函数形式）的基本原理是：多个正余弦波叠加（蓝色）可以用来近似任何一个原始的周期函数（红色）。
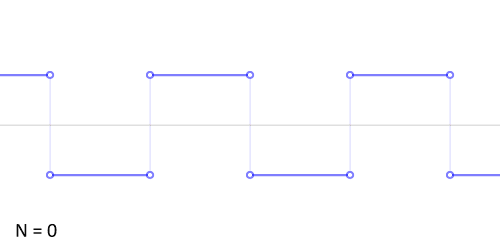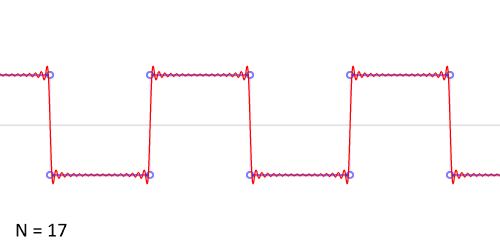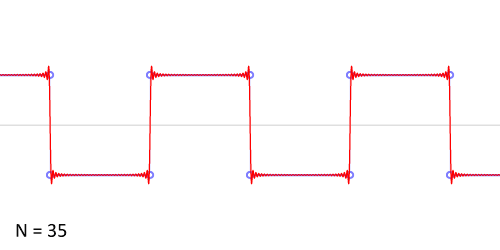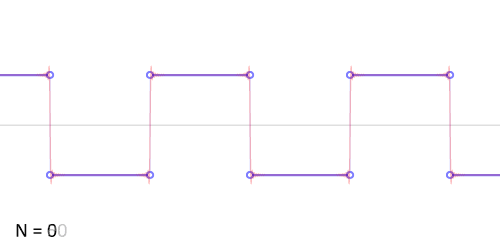
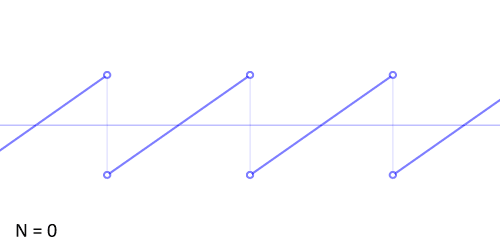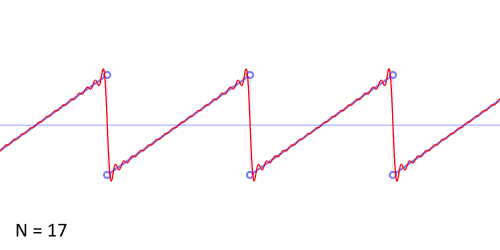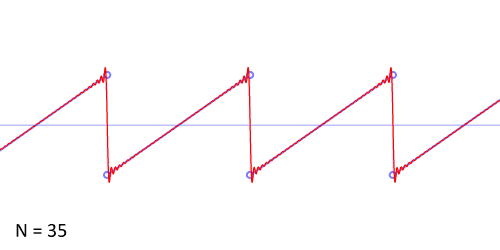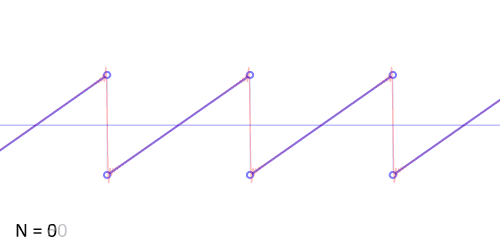
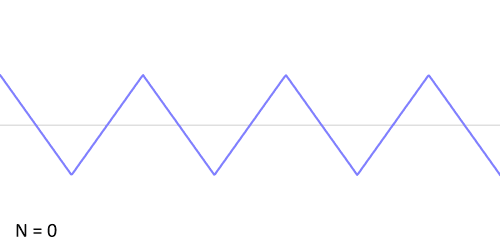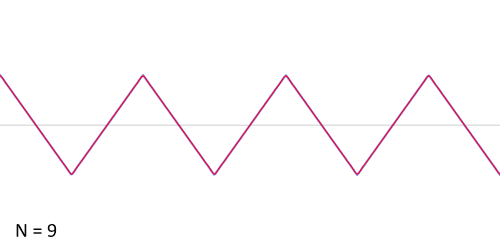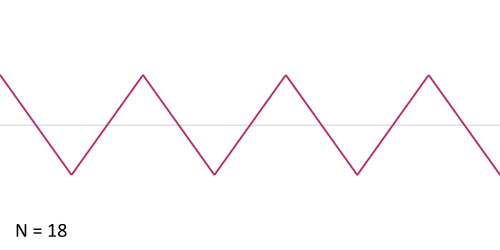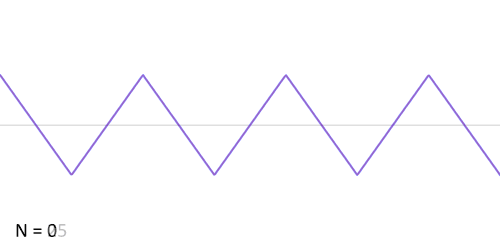
几个傅立叶分解实例，用波叠加出分段函数。
图片作者：LucasVB
超模君，你讲了这么多，我还是没听懂。。。
既然这样子，超模君换个说法：
其实，当我们去买菜的时候，各种蔬菜都不一样，但都能转换成“n个1斤砝码+m个1两砝码”的组合。
此时，那我们把上图末尾处蓝色的竖线就想象成3个1号波+5个2号波的组合等等。
一下子计算就简单许多了，使得积分，微分，成了最简易的计算：加减乘除。在处理上有多方便就不用说了……
因此，傅立叶变换在数学里面，这本身就是一种解微分方程的方法。
也正因为傅立叶变换有趣的简化方式，使得傅立叶变换成为工程和物理领域里最重要的数学公式之一。
