三角形作图题中经常出现“两条边的比值为p:q(或m:n)”这一条件。于是我们可能会想到阿波罗尼圆,因为阿波罗尼圆是到两个定点距离的比值是定值的点的轨迹。于是,下面两道类似题目的解法就都有可能用到阿波罗尼圆。我们一起来讨论一下。之前讲三角形作图题共讲了15道,所以,今天的两道就叫做第16和17题。
第16题:已知a,∠A,AB:AC=c:b=m:n,求作三角形ABC。
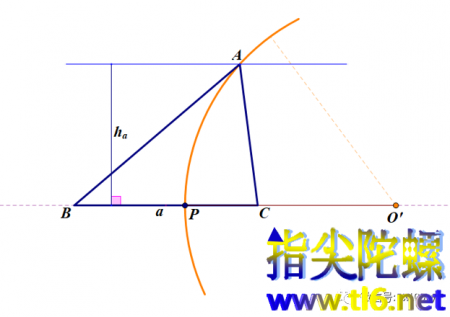
第17题:已知a,ha,AB:AC=c:b=m:n,求作三角形ABC。
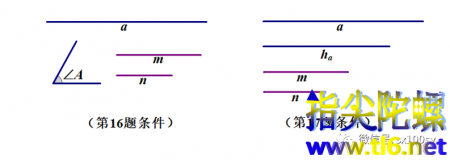
注意,已知m:n,可以认为已知两线段,其长度分别为m和n。下面作图中不妨假设m>n。
第16题解答:由已知的a和∠A(大小设为α),可以作出长度为a的弦及其内接角为α的圆弧(也叫做含角α的弓形弧)。如下图所示。图中BC=a,为弦,而圆弧BA'C即为弦BC上含角α的弓形弧。本题的关键是要确定三角形顶点A的位置,这个位置是一个点,它可以由两条不同的轨迹来确定。目前它一定位于弓形弧这条轨迹上,所以还需找到另一轨迹。这就要用到“AB:AC=m:n”这一条件了。
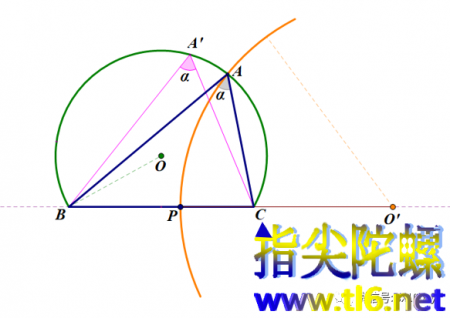
如上图所示,我们来确定出线段BC的定比分点(定比为m:n)。在线段BC内确定一点P,使BP:PC=m:n,在BC的延长线上再确定一点Q(图中未画出,因为可能较远),也使BP:PC=m:n。具体确定定比分点的方法,这里不再具体写出(用到《线段的作图——代数解析法》那一讲中作线段方法的第4条)。找到P和Q之后,以线段PQ为直径作圆,这个圆就是所谓的阿波罗尼圆。这个圆一定与刚才所作的弓形弧有交点,那么这个交点就是所要求作的三角形的顶点A。总结:本题所用方法可以称作轨迹法。两条轨迹,一条是弓形弧,一条是阿波罗尼圆,于是就可以找出它们的交点。
第17题解答:与第16题的解题思路类似,不同之处就是上题的弓形弧换成了本题的一条到BC距离为ha的直线。直线与阿波罗尼圆的交点就是点A。见下图。