梅涅劳斯定理证明蝴蝶定理
上传时间:2021-03-08 16:17点击:
蝴蝶定理:AB为圆O的任意一条弦,M为AB的中点,CD和EF为过点M的两条不同于AB的弦。连接CF,DE,这两条弦与AB交于点G和H。那么,GM=MH。证明:如下图所示。
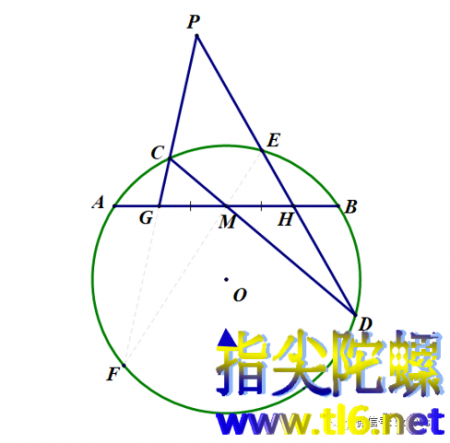
根据梅涅劳斯定理,有
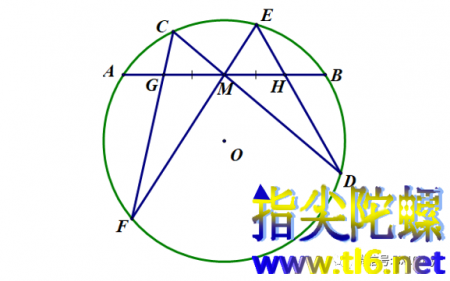
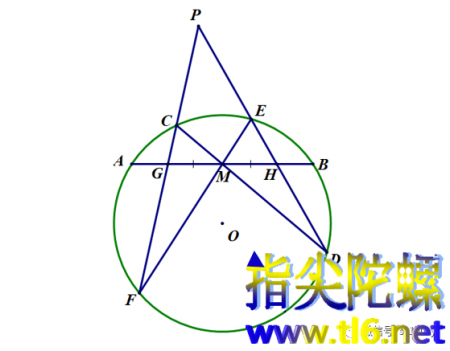
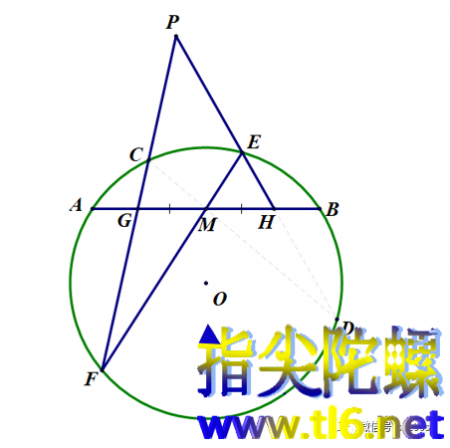
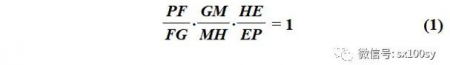

根据梅涅劳斯定理,有

(1)式乘以(2)式,并通过演变(其中用到割线定理、相交弦定理等),最终可得出结论,如下所示。

证毕。



















