今天讲一个漂亮的图形,请先看一看它的动画。
(1)西姆松线 从三角形外接圆上一点P向三角形三条边引垂线,三个垂足一定位于一条直线上。这条直线就叫做西姆松线。
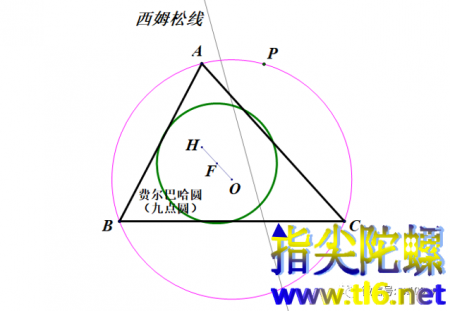
随着点P在外接圆上运动一周,西姆松线朝反方向旋转半周(可再次观看上面的动画)。西姆松线的包络是一个“尖点三角形”。这里的包络是指,尖点三角形的切线都是西姆松线,而每一条西姆松线都是尖点三角形的切线。你观察一下看。
(2)费尔巴哈圆 上图中,点H为三角形ABC的垂心,点O为三角形外接圆(图中粉色)的圆心。垂心H和外心O连线的中点F为三角形的费尔巴哈圆(即九点圆,图中绿角)的圆心。费尔巴哈圆的半径是外接圆半径的一半。这些以前都讲过,可以查阅以前的文章(链接见文后)。
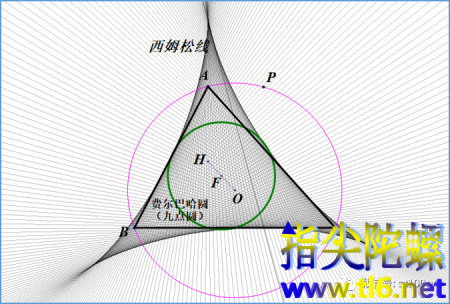
(3)三点内摆线(圆内旋轮线) 如下图所示,以费尔巴哈圆的圆心F为圆心,以费尔巴哈圆半径的三倍为半径作一个圆(图中蓝色)。两圆是同心圆。
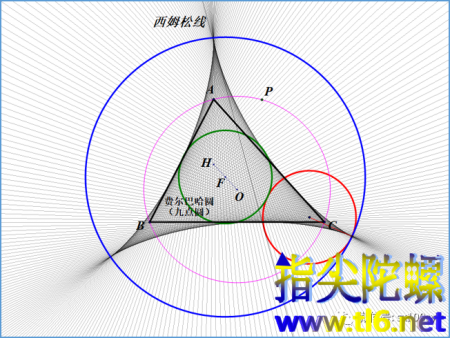
那么,在两个同心圆之间正好可以放进一个同费尔巴哈圆一样大小的圆(图中红色)。让两同心圆之间的这个圆(动圆)在大圆内侧无滑动地滚动(费尔马哈圆不影响这种滚动),则动圆上一个定点运动的轨迹是一个内摆线,也叫做圆内旋轮线,“尖点三角形”(图中黑色阴影区域的轮廓)。动圆上的点在画出尖点三角形的三条“边”后正好回到出发点,这是因为大圆与小圆的半径之比是3:1,从而周长之比也是3:1。让红色动圆与蓝色大圆的切点位置选择合适,就可以使得这个轨迹与前面所说的包络完全“重合”。
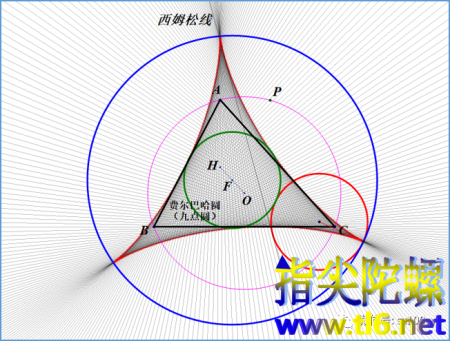
费尔巴哈圆位于这个尖点三角形内部,且与之相切。
[1]《费尔巴哈定理|内切圆|旁切圆|九点圆》
[2]《九点圆最简洁的构造和证明》
[3]《再谈九点圆——从轨迹的角度》
[4]《位似变换|欧拉线|九点圆》
[5]《九点圆的证明》
[6]《九点圆与欧拉线》
[7]《已知四点画双曲线》
[8]《丰富多彩的九点圆》



















