今天讲一个轨迹题,我们将用笛沙格定理证明这个轨迹是一条直线。
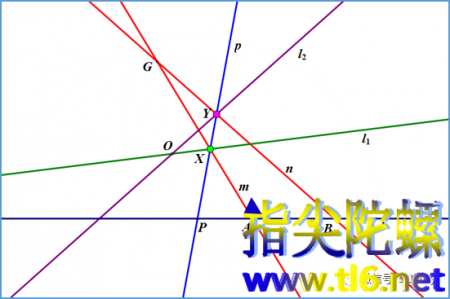
题目是这样的:有两条相交直线l1(绿色)和l2(紫色),交点为O。另有一条直线l(深蓝色),其上有三个定点P、A和B。过点P作直线p(天蓝色),与直线l1和l2分别交于两点X(绿点)和Y(粉点)。如上图所示。过直线l上的点A和直线l1上的点X作直线m(红线之一);过直线l上的点B和直线l2上的点Y作直线n(红线之二)。两直线m和n相交于点G。当直线p绕着点P旋转时,按上述方法得到的点G也将随之运动。那么,结论是,点G的运动轨迹是一条直线。下面是运动过程的动画演示。
证明非常简单。首先,直线p转动到过点O时,AO与BO的交点就是点O,所以,点O必定在轨迹上。下图中,点G当然也在轨迹上。我们连接过G和O的直线GO(图中黑色)。再随便作一条过点P的直线p'(下图中另一条天蓝色直线),它与l1和l2分别交于点X'(绿色)和Y'(粉色)。连接点A和X',再连接点B和Y',得到两直线m'和n'(均为褐色)。设这两条直线m'和n'相交于点G'。由于直线p'是任意的,所以,只要证明点G'位于直线GO上,就可以证明我们所要的结论。
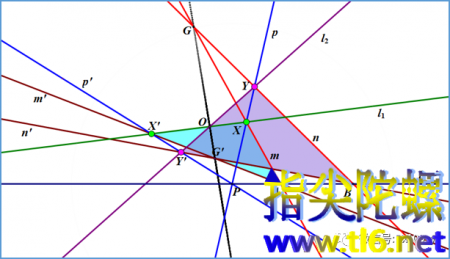
观察上图,我们选择三角形AXX'(青色)和BYY'(浅紫色)(两三角形可能有重叠,不影响讨论)。规定它们的三组对应顶点分别为A和B,X和Y,X'和Y'。这三组对应顶点的连线AB、XY、X'Y'显然相交于点P。所以,根据笛沙格定理,两个三角形三组对应的边AX和BY,XX'和YY',X'A和Y'B的交点G、O、G'一定位于一条直线上。所以轨迹为直线,如图中GOG'(黑线)所示。证毕。
本题利用了笛沙格定理中的“三点共线”结论。那么显然,两点就可以确定一条直线,而让第三点动起来,从而形成轨迹——直线。



















