今天讲一个从椭圆外一点作椭圆切线的绝妙方法
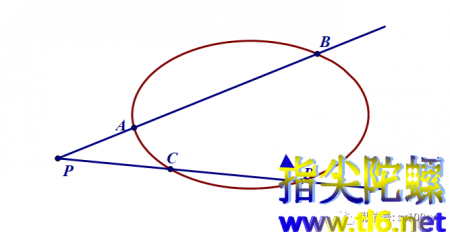
我们只知道一个“祼椭圆”和椭圆外一点P
如下图所示

我这里所谓“裸椭圆”是指椭圆本身,而它的中心、焦点、顶点、准线一概不知
所以适合用射影几何学的方法
射影几何学的方法非常简单,但方法背后的理论就会比较深奥
我先来讲一讲作法
(1)过点P作两条椭圆的割线,两条割线分别与椭圆交于点A、B和点C、D
如下图所示
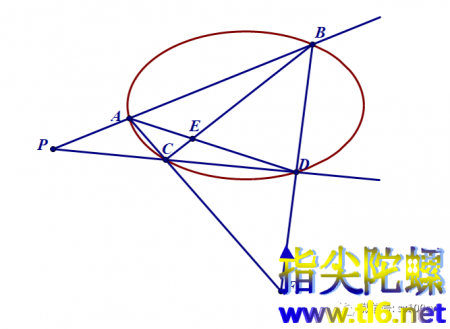
(2)作过点A和D的直线,再作过点B和C的直线
两条直线相交于点E
如下图所示
(3)作过点A和C的直线,再作过点B和D的直线
两条直线相交于点F
如下图所示
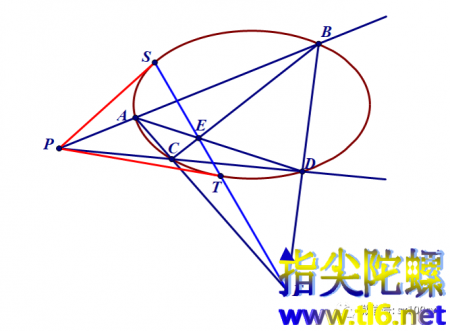
(4)作过点E和F的直线(下图中蓝色)
因为点E位于椭圆内部,所以,直线EF一定与椭圆相交于两点
设这两点为S和T
(5)那么,椭圆上的这两个点S和T就是从圆外的那个点P向椭圆所作切线的切点
最后连接PS和PT,就得到所求作的两条切线(下图中红色)
作图完毕
注意,上面作图过程中,所作过点P的两条割线是任意的
但这个任意性并不影响点E和点F永远位于一条确定的直线上
我们知道,点P和椭圆一旦位置确定,那么过点P的两条切就是确定的,两个切点也是确定的
从而过两个切点的直线就是一条确定的直线
那么,从点P所引的任意两条椭圆割线,交出的四个点构成一个椭圆的内接四边形
则这个四边形除有一组对边所在直线相交于点P外,另外一组对边所在直线的交点及四边形对角线的交点都位于定直线上
这个就是我们前面作图的理论依据
这个依据也可以当成一条定理,它的证明有些复杂,但也是可以接受的,这里就不介绍了
我们这里不过是反过来先确定这条定直线上的两个点,再连线找出直线与椭圆的交点即切点



















