今天通过两个著名的定理——帕斯卡定理和布里安香定理——来讲一讲射影几何的内在美:有帕斯卡定理存在就一定有布里安香定理存在,反之亦然。两个定理是配极对偶的。以椭圆为例,对圆锥曲线都正确。
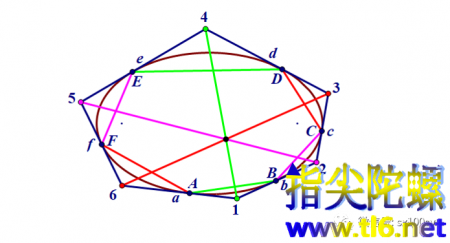
ABCDEF为椭圆的内接六边形。a,b,c,d,e,f分别为椭圆在点A,B,C,D,E,F处的切线。六条切线围成一个六边形,它是椭圆的外切六边形,用abcdef表示(用顶点表示就是123456)。内接六边形与这样得到的外切六边形是配极对偶关系。即,内接六边形的边(所在直线)配极对偶到外切六边形的顶点,比如“直线AB”到“1”,即“直线AB”与“1”是椭圆的极线与极点;内接六边形的点配极对偶到外切六边形的边,比如点A与边a所在直线就是椭圆的极点与极线的关系。
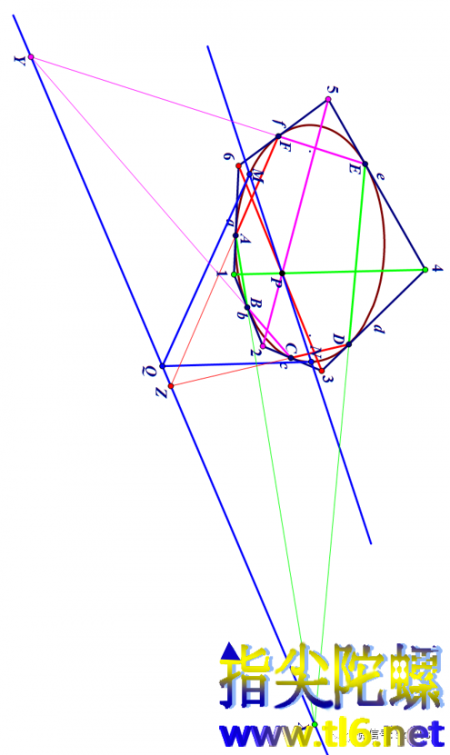
帕斯卡定理说,椭圆内接六边形三组对边交点X、Y、Z(下图中未画出,最后一张图有)共线。具体来说,AB与DE是内接六边形一组对边(图中绿色),过AB的端点A的切线a与过端点B的切线b相交于点“1”,则点“1”与AB所在直线就是极点与极线的关系。同理,点“4”与直线DE也是极点与极线的关系。

从而,帕斯卡定理中“对边交点”(比如AB与DE的交点X)就配极对偶到布里安香定理中的“相对顶点连线”(“1”与“4”的连线“14”)。

我们把这两个互为配极对偶的定理具体写出来,供您对比(注意两定理中相同颜色的短语,它们之间是对偶关系)。
帕斯卡定理:
椭圆内接六边形ABCDEF的三组对边(AB与DE,BC与EF,CD与FA)的交点X、Y、Z共线。
布里安香定理:
椭圆外切六边形abcdef的三组对顶点(“1”与“4”,“2”与“5”,“3”与“6”)的连线“14”,“25”,“36”共点。
最后,帕斯卡定理中三点共线之线与布里安香定理中三线共点之点也是配极对偶的,即极线与极点关系。如下图所示,点P与直线XYZ是极点与极线的关系:过极点P的任意一条直线与椭圆有两个交点M和N,则点M和N处的切线的交点Q正好位于点P的极线XYZ上。或者说,让过极点P(布里安香定理中三条对角线交点)的直线绕点P转动,直线与椭圆的两个交点处椭圆切线的交点Q的轨迹位于点P的极线(帕斯卡定理中三组对边交点所共之线)上。