已知椭圆的五条切线，求作这个椭圆
上传时间：2021-04-29 11:28点击:
今天讲由5条切线作椭圆。在射影几何中，帕斯卡定理与布里安香定理是对偶的。从而内接六边形与外切六边形对偶。点与线对偶，对边与对顶点对偶，共线与共点对偶，……。所以今天的作图就与上期的对偶。
具体来说，先给5条切线依次取名1，2，3，4，5。这里，名称既可以表示整条切线也可以表示切于同一点的外切六边形的边。于是，切线1与2的交点就自然地叫做（1，2）。其他类似。
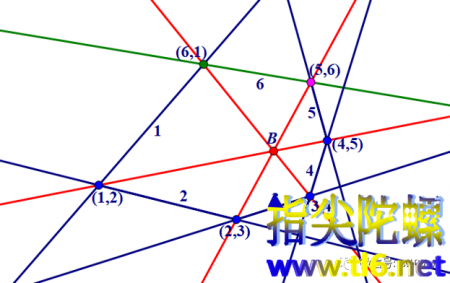
不妨在边5上取一点，这个点可动。但现在先固定它让它不动。第6条切线将经过这个点，所以，这个点就是（5，6）。现在根据布里安香定理，我们作过外切六边形对顶点的直线（虽然外切六边形还不确定，但有两条对顶点连线是可以作出来的）。具体来说，作连接点（1，2）和（4，5）的直线；再作过点（2，3）和（5，6）的直线。两条直线相交于点B（布里安香点）。那么过第三对对顶点的直线也应该经过点B。而目前我们知道点B和第三条对角线经过点（3，4）。所以过点（3，4）与点B的直线将与切线1相交于一点，这个交点就一定是外切六边形的一个顶点，即（6，1）。于是过点（6，1）与（5，6）的直线就是第6条切线。
最后，让动点（5，6）动起来，我们也就让第六条切线动起来，那么，这条动切线的包络就是一个椭圆。如下图所示。注意，其中椭圆左侧的切线没有画全，这是因为动点要运动到切线5的很远至无穷远的地方才能做到。
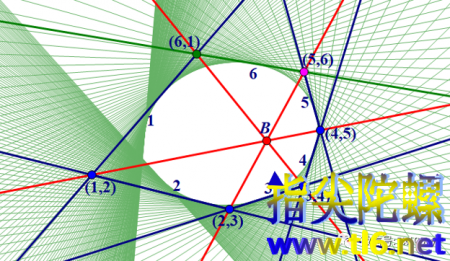
椭圆（其实对圆锥曲线都对）可以表示成点的轨迹，也可以表示成切线的包络。点的轨迹与切线的包络也是对偶的关系。数学之美在此得以完美展现。
