对于大多数题目来说,不太会单独使用乘法原理和加法原理,通常都是综合运用。
一般的形式为:做一件事情,有N个步骤,每个步骤里又各自有不同的分类,每个分类里又有多种方法;又或者是,做一件事情,有N个分类,每个分类里又有不同的步骤,每个步骤里又有多种方法。
总之,需要小朋友熟悉乘法原理和加法原理,并加以综合运用。
1
小明放学先去体育馆,再回家。从学校到体育馆有地铁、公交车、出租车这三种方式,从体育馆到家有出租车、步行这两种方式。地铁有2条不同的线路可以选择,公交车有3条不同的线路可以选择,出租车有4家不同公司的可以选择,那么小明从学校先去体育馆、再回家,总共有多少种走法?
这道题可以看成两个步骤:
①从学校到体育馆
这个步骤里有3个分类:地铁、公交车、出租车,每个分类分别有2、3、4种方法,需要运用加法原理
②从体育馆到家
这个步骤里有2个分类:出租车、步行,每个分类分别有4、1种方法,需要运用加法原理
但是两个步骤,需要运用乘法原理,所以综合起来列出的表达式为:
( 2+3+4)×( 4+1)=45
2
如下图,小明要从A点走到C点,要求所有的线路和点都不能重复走,那么有几种走法?
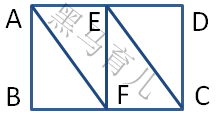
这道题如何做?通过有序思考(《【二年级】有序思考》)穷举?你可以让小朋友先尝试做一下。
我试过几次,太容易遗漏了,最终我总共数出9条,你让小朋友自己对比一下,看看自己遗漏了哪条:
ABFC、ABFEC、ABFEDC、AFC、AFEC、AFEDC、AEC、AEDC、AEFC
可以看出来,在一个稍微复杂没有明显规律的图形中,运用有序思考很难做到不遗漏,所以我们可以换个方法试试。
对于这个题目来说,我们可以观察出,从A走到C,必然经过E或者F,甚至两个点都经过,所以我们可以分成两类:先经过E、先经过F
①先经过E
先经过E,我们就可以视作2个步骤:
第一步,从A到E,只有1条路;第二步,从E到C,有直接到C、经过F、经过D这3条路
根据乘法原理,总共有1×3=3条路线
②先经过F
先经过F,我们也可以看成2个步骤:
第一步,从A到F,有直接到、经过B这2条路;从F到C有直接到、只经过E、经过ED这3条路
根据乘法原理,总共有: 2×3=6条线路
所以总共有:3+6=9条
3在正方体骰子的6个面分别写上1~6,有2个这样的骰子掷出以后,朝上的那面数字之和为偶数的有多少种情况?
先来分析一下,每个骰子朝上的那面都可能是1~6中的任意一个数字,但如果两个数字之和为偶数,我们知道必须是2个奇数,或者2个偶数,如果是一奇一偶,他们的和不可能是偶数,所以我们要分2类来看。
①两个都是奇数
第一个骰子是奇数的可能只有1、3、5三种,第二步,我们掷出第二个骰子,也是1、3、5三种,所以根据乘法原理,总共有3×3=9种情况
②两个都是偶数
第一个骰子是偶数的可能只有2、4、56三种,第二步,我们掷出第二个骰子,也是2、4、6三种,所以根据乘法原理,总共有3×3=9种情况
根据加法原理,这两类的情况相加,总共有18种情况。



















