今天简单地讲一讲梅森数及梅森素数。不可能涉及梅森数的方方面面,而只是讲一讲比较好理解的方面。形如
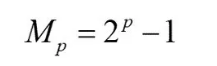
的数叫做梅森数,其中p为素数。
就算梅森数的定义中要求p是素数,也不能保证梅森数一定是素数。梅森数可能是素数,也可能不是素数即合数。我们列出p取前面一些素数时的梅森数,并指出它们是素数还是合数。

从上表看,好象素数多于合数。其实不然。上表若再往后列出,素数的情况就远少于不是素数的情况。目前已经证明了,梅森素数的个数是无穷多的。而梅森数列变大的速度非常之快,所以,通过梅森数,数学家们可以更加容易地发现更大的素数。
梅森数定义中的p为素数。那么为什么不考虑p为合数的情况呢?是这样,若p为合数,则(2^p-1)一定是合数,而我们更关心的是梅森素数。为什么p是合数时(2^p-1)一定是合数呢?可以分两种情况讨论。第一种情况,p为偶合数,则(2^p-1)是平方差的形式,当然是合数。第二种情况,p为奇合数,不妨设p=mn,则有
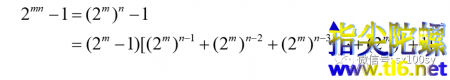
所以它也是合数。于是,梅森数定义中就只规定p是素数。
(以上p为奇合数的情况的说明,回答了上次那位朋友的留言。感谢这位读者。! )
)
因为梅森素数很快就变得很大很大,并且后一个梅森素数比前一个梅森素数要大上很多很多,所以,稍微大一点的梅森素数动辄就有几十位、几百位甚至几千位,......。今天我就讲一讲梅森素数位数的计算。(其实就是梅森数的位数的计算。)
以p取521为例。已经证实,p=521时的梅森数是素数:
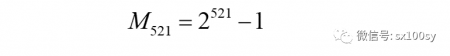
它是一个具有157位的正整数,这已经是一个很大的数了。但因为素数有无穷多,所以,这个157位的素数也真的不算大,或者说很小。一般来说,我们常用的计算器是显示不出完整的157位的这个梅森素数的。其实我们也没有必要写出这个157位的素数来。但是,这个157位数的“157”,是怎么知道的呢?算出一个梅森素数有多少位,倒是一个很有趣的事情。这并不难办到。我们下面就来算一算M521这个梅森素数的位数。
首先,我们要说明,梅森素数
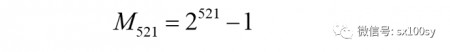
与它的下一个正整数(即比它大1的正整数)

具有相同的位数。因为若不具有相同位数,而后者又比前者大1,那么,前者就一定是以0结尾的正整数。但是,2的正整数次方都是以2,4,6或8结尾的,所以,梅森数M521是以1,3,5或7结尾的,不可能以0结尾。也就是说,梅森素数M521加1后,不足以增加位数。于是,我们要计算梅森素数M521的的位数,只需计算2^521的位数就可以了。
给“2的521次方”取以10为底的对数,得到
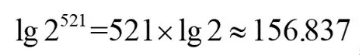
把对数式转换成指数式,得到
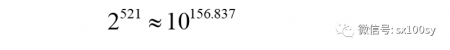
“10的156次方”是一个具有157位数字的正整数,并且是所有具有157位数字的整数中最小的一个:
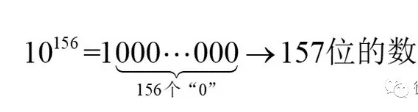
“10的157次方”是一个具有158位数字的正整数,并且是所有具有158位数字的整数中最小的一个:
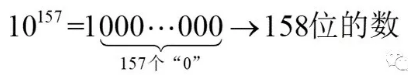
由于
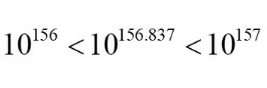
所以,

梅森数为形如下面这个样子的数(其中p为素数):
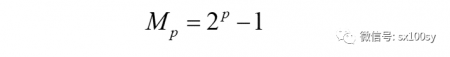
梅森数可能是素数,也可能是合数。下面我们要讨论的是梅森素数与完全数的关系。那么需要先说一说什么是完全数。
先说前几个比较小的完全数。“6”是第一个完全数,因为6除自身以外的因数1,2,3的和仍然等于6。第二个完全数是28,因为28除自身以外的其他因数之和为1+2+4+7+14=28,即等于自身。下一个完全数是496,请您自行验证。
那么,完全数的定义就是:除自身以外的其他因数之和等于自身的数称为完全数。
人们对一个新定义的数总是要去找一找它自身的规律。人们发现:
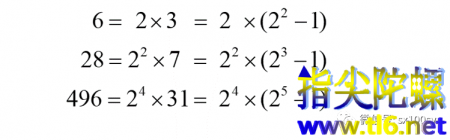
这是前三个完全数。从这三个数可以发现什么规律呢?我们试着归纳一下,应该是下面这个规律:
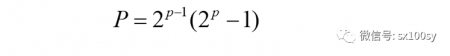
(注意,用P表示完全数是因为完全数的英文是PerfectNumber。)上式中小写p分别取前三个素数2,3,5时,上式的第二个因数分别是(2^2-1),(2^3-1),(2^5-1),它们分别等于3,7,31,正好就是前三个梅森素数。那么,我们试着看一看p取素数7时情况。这时P的表达式中第二个因数为(2^7-1)=127,是第四个梅森素数。而这时的P可以通过上面公式计算出来:
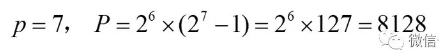
我们来看一看这个8128是不是完全数。把这个数除自身以外的因数加起来:
1+2+4+8+16+32+64
+127+254+508+1016+2032+4064
=8128
所以,我们又发现了一个完全数,即8128。
梅森素数与完全数有了很紧密的联系。那么,是不是只要给定一个梅森素数,按照下面这个公式
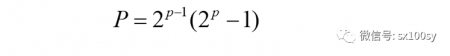
就可以得到一个完全数呢?答案是肯定的。也就是说,上式中右侧的(2^p-1)若是梅森素数,则按上式得到的P就一定是完全数。我们下面就来证明。
上式是两个数的乘积,其中第一个数是“2^(p-1)”,另一个数是梅森素数(2^p-1)。寻找P的不同的因数并不困难。我们来看一看具体怎么做。
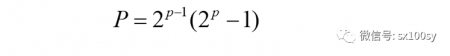
设上式中的第二个数即梅森素数(2^p-1)=q。于是,P的所有因数为:
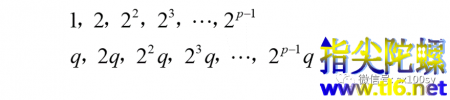
注意,上式中最后一个因数是P本身。
我们把除自身以外的一切其他因数加起来,就相当于把一切因数加起来再减去自身。于是得到

即P除自身以外的因数相加,结果等于P。这说明P是完全数。
我们前面的证明是说,只要P的表达式中“第二个因数”(暂且把2^(p-1)当成第一个因数)是梅森素数,则P就是完全数(当然是偶完全数)。其实,现在也已经证明了,若一个数是偶完全数,则它一定可以写成下面这个形式:
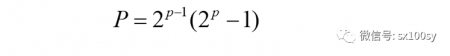
其中的“第二个因数”是一个素数。而“第二个因数”是梅森数的形式,所以,第二个因数一定是梅森素数。也就是说,一个偶完全数一定可以写成一个梅森素数与2的方幂乘积的形式。或者说,梅森素数与偶完全数是一一对应的。这个公式是欧几里得发现的,多少个世纪过去了,才被后来的欧拉证明是偶完全数的唯一的公式,即任何偶完全数都具有这个形式。
上面我们只说是“偶完全数”公式。那么,是不是存在奇数的完全数呢?目前这是一个世界级的难题,可能还没有被解决。谁能解决它,谁就了不起。解决它是说,或者找到一个奇完全数,或都证明不存在奇完全数。这个难题可能很难很难!



















