2019年11月26日联合国教科文组织第四十届大会上正式宣布3月14日定为国际数学日。之所以选择这一天,是因为连接“天圆”和“地方”的圆周率近似为3.14。

电视上经常有小孩子背诵圆周率的表演,其所表现出的记忆力令人叹为观止,但是这死记硬背怎么也追不上电脑的机械计算。
2021年8月19日,瑞士的格劳宾登州应用科学大学(UniversityofAppliedSciencesoftheGrisons)的DAViS团队宣布完成π到62.8万亿位(62,831,853,071,796位)的计算。计算花了高性能计算机108天9个小时。
62.8万亿位是什么概念呢?一般正16开的版面可约排1400个5号字,62.8万亿需要448.6亿个16开的版面,每个中国人可以分到32页(2021年中国人口14.13亿)。
人类历史上寻找π的值则反映人类勇于探索和开拓进取的精神。
据考证公元前1900–1600年的巴比伦时代,已经有π=25/8=3.125的记录了。

我们祖冲之(公元480年)则推到355/113=3.1415929,即小数点后六位精度。这个领先地位一直保持了800多年。
牛顿(公元1660年)把其精度推到小数点后15位。
在1706年,梅钦(JohnMachin)给出了近似式
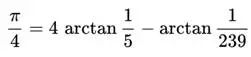
其精度可达100位。
现代则是用计算机编程计算。如何构造巧妙的算法,用计算机近似计算π,确实是很好的挑战。
牛人冯·诺依曼用当时的ENIAC计算机算了70个小时,实现了2037位精度。
目前最好的精度就是上面DAViS团队的计算。
这种追求情怀当然是国际上少数π铁粉的行为,不过,尽管是少数,但仍有铁粉,然而国内却没有“民科”做这事。这大概因为:
1)需要编程(民科往往不会);
2)不能乱说(因为有事实的数据,民科无法信口开河);
3)近似计算理论需要扎实的数学功底(民科对这个最扎心)。
与π铁粉的屈指可数相比,相对论的民科专家可就多了去了。几年前引力波时髦起来,国内有个初中生就蹭“引力波的预测”。其实爱因斯坦在提出广义相对论不久,自己就研究了这个问题,起初他认为引力波是不存在的,不过他不是像我们初中生那样靠“感觉”来预测,而是基于公理化体系的复杂推导(民科最烦这个,看看国内民科的文章有什么推理或冗长的数学推导?)。当文章送到编辑部让审稿人审时,审稿人很仔细地重复了爱因斯坦推导过程(我们民科的文章能让审稿人重复吗?),发现推导过程有错误,杂志便把文章退了。后来“匿名”审稿人鬼使神差地与爱因斯坦本文一起又重新推导一遍,修正了推导过程中的错误,结论变为:引力波是存在的。
背诵圆周率虽然没民科那么不着调,但精神也偏离公理化、偏离逻辑习惯。
目前国内背诵圆周率吉尼斯记录保持者是吕超。在2006年11月20日14时56分,他成功背诵π小数点后面67890位(大约48.5页16开版面),总共花去24小时零4分钟。国际吉尼斯记录是印度人RajveerMeena在2015年3月21日取得的,背诵到了70000位(花了近10个小时)。
这个位数离上面计算机算出62.8万亿位差远了,还要继续背下去吗?至于鼓动死记硬背热情的媒体人,智商也应该100分了吧。