摘要:落体偏东和抛体偏西两个问题一般用科里奥利力来分析,这往往变成一个死记硬背的刷题行为(如果从头介绍科里奥利力,那么教学成本也很高)。本文给出不涉及科里奥利力的概念,但又足够简洁的分析方法。
〇、引言
落体偏东是这样物理现象:物体从距地面一定高度自由下落时,落地点会比最初下落位置稍微偏东。这是个有趣现象,历史上也是地球自转的证据之一(如果不能证明地球自转,我们还得生活在地心说的教义中)。
对落体偏东的理论分析,通常使用科里奥利力(Coriolisforce)。但是:
1) 科里奥利力需要相对坐标系和非惯性系的概念;
2) 科里奥利力没有施力物体,所以学生理解起来就有点别扭。物理教学中,一谈到力,就想到力是物体之间的相互作用,既有受力物体,也有施力物体。
以上两点都会增加落体偏东的理解门槛和学习成本。
本文所采用的分析避开科里奥利力,但又足够简洁。
一、定性分析
下面对落体偏东定性分析。因为是定性分析,所以以在赤道处落体为例,这是最简单情形。
在下面图1中,赤道上方有一高度为h的垂直立柱。此立柱随地球表面一起绕地心转动。显然,柱顶的速度大于柱底的速度。
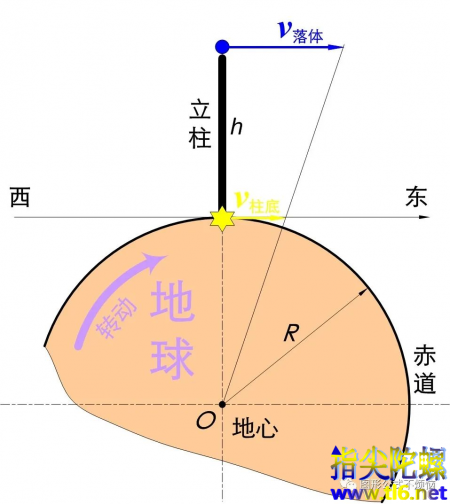
图1
落体待在柱顶时,其速度与柱顶速度相同(方向与立柱垂直),也比柱底的速度大。
从立柱上掉落后,由于地球引力,它会获得向地心的速度,这个分量越来越大(图2)。在掉落过程中,落体从柱顶获得的速度依然存在,而且一直大于柱底的速度。
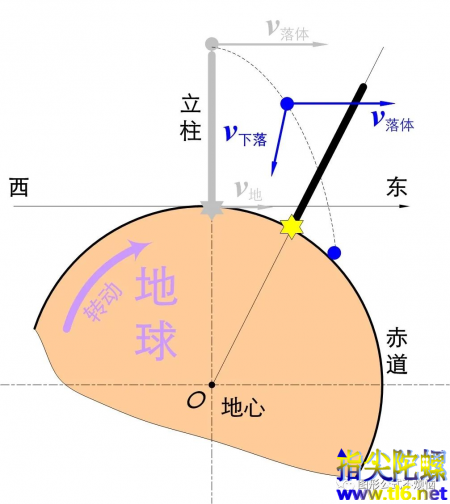
图2
落体和柱底都有向东的速度,但前者大于后者,所以等到落体落到地面上时,它跑到了柱底的前方,也就是在柱底的东边。这即所谓的落体偏东。
抛体运动的分析类似。在图3中,抛体的水平速度与地球表面速度相同。
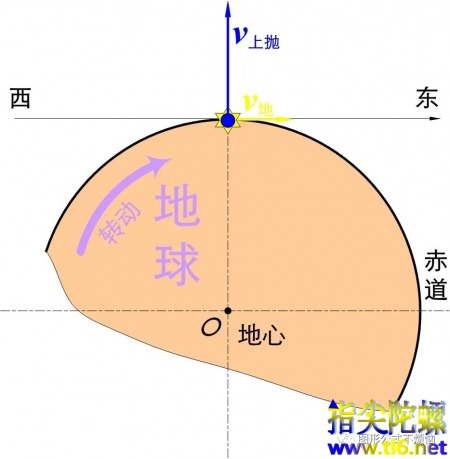
图3
想象有个像图1中那样垂直于地面的虚拟立柱,它随地球转动,如图4中所示。
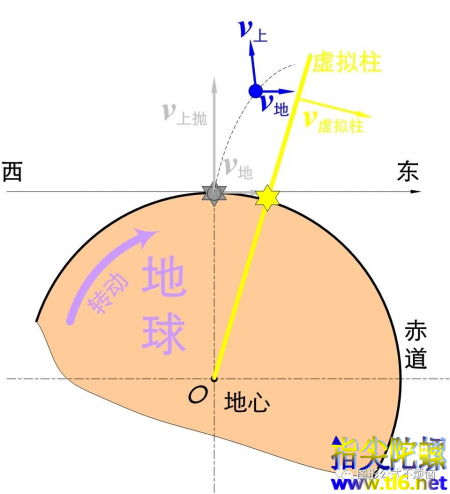
图4
当物体抛到空中后,其最初获得的V地小于位于虚拟立柱同等高处的速度V虚拟柱。这个小于号是从抛体离开地球表面就开始的,所以抛体始终落在虚拟柱的后面。
当抛体升高到最高点后开始下落(图5)。
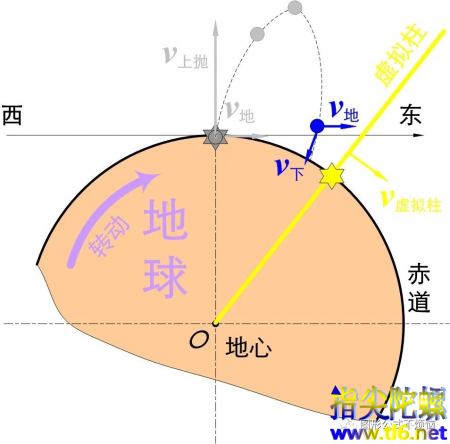
图5
在下落过程中,抛体最初获得的V地分量依然小于同等高度虚拟柱上的V虚拟柱,所以抛体落后于虚拟柱的距离进一步加大。
等抛体回落到地面,虚拟柱底(也就是开始抛的地面位置)位于抛体落回的东边。这就是抛体偏西的现象。
二、定量分析有“纠结”
我们来看一下,上一节的定性分析能不能简单地变成定量结果。
不管是落体,还是抛体,其立柱相对于地球半径都很短,所以地表弧段可以近似为线段。因此,落体的位移差可近似为

四、消除“纠结”
落体偏东的量很小。假定落体从h=100m处落下,偏东的距离也就只有21.9mm(图1-图5都画得很夸张)。所以,我们也很自然地认为重力加速度方向是不变的。
然而,抛体在空中运动时,重力加速度指向球心,所以其方向肯定要变,尽管变的幅度很小。很小的幅度会不会有影响呢?要知道偏东也就只有21.9mm,所以还是需要考虑重力加速度方向的微小变化。
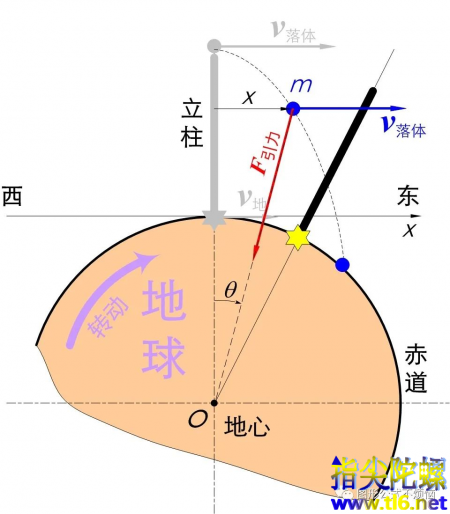
图6

方程(€4)是微分方程,可以迭代近似求解。
首次近似,就像第二和第三节那样,取

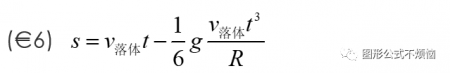
可以将式(€6)作为方程(€4)的右边s的近似值,重复上述操作,得到精度更高的近似解。所得结果是对(€6)修正,相应修正项是t的5次项。因为落体t的范围很小,不用再计入高次项了(这当然是知道了答案的“凑"),所以止步于式(€6)。
从式(€6)可得

我们再来看抛体,此时(€4)同样成立,但是第一轮近似为s≈v地t。这样有



有人可能对上述近似处置觉得不保险,那么就必须要解微分方程。
微分方程(€4)可类比振动方程



回过头再看第二节,它对落体处理还是有瑕疵的,因为重力加速度不垂直所导致的水平速度是减小V落体(最终答案也确实减少了1/3),但是我们没有(能)讨论这个减小不会影响定性结果(如果你有,请留言)。
对抛体的定性没有影响,因为重力加速度不垂直所导致的水平速度进一步减小了V地。
五、科里奥利力的途径
为了完整,最后来看一下采用科里奥力的处置。
考虑地球自转,固定在地球表面参考系不再是惯性系,而是绕地球南北极轴转动的参考系。质点在地球表面参考系有相对运动时,只有加上因坐标系转动所导致的离心惯性力和科里奥利力之后,才能用牛顿第二定律。
离心惯性力与地球自转的角速度平方成正比,科里奥利力与地球自转角速度一次方成正比。因为地球自转角速度很小(7.292x10-5rad/s),所以离心惯性力相对科里奥利力可以忽略不计。
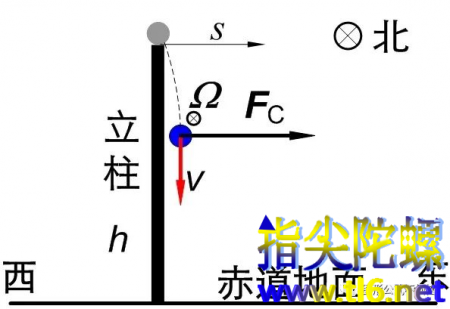
图7
科里奥利力FC=-2mΩⅹv。对从赤道上方下落的物体,FC的方向指向东(图7),大小为FC=2mΩv(前面已经指出,v并非竖直向下。但是其偏度的影响可忽略不计),这样下落过程中沿水平方向有


对于抛体,上抛过程的科里奥利力向西,下落过程的科里奥利力向东,二者对称,所引起的加速度也是对称的。但是,位移要对加速度积分两次,所以位移不会抵消为零。
在上升段(向东为正向)




结果与第四节相同。
六、结束语
本文对落体偏东和抛体偏西进行了定性和定量分析,分析过程较为简洁,理解门槛也比较低。