疫情可能让很多人丢掉了工作,但却让另一拨人忙得热火朝天,他们不是英雄而是骗子。
“杀猪盘”骗局在不方便出门的隔离期间成为了骗子们炙手可热的一种套路,毕竟疫情大环境下,很多人工作不顺利,情感也更为空虚,而“见光死”骗子们也有了不见面的最好理由。

所谓杀猪盘,简单来讲就是利用话术博取受害者的信任,骗其加入一些非法的赌博或投资平台,从小投入获小利润,慢慢加大投入,甚至让受害者借高利贷来加大投入。
这种一步一步获取信任的过程就被称作是“养猪”,最后卷款就是“杀猪”。
受害者以女性为主,少则被骗三五万,多的数十万上百万不止,还背了一屁股债。
如果有了解过具体被骗案例,恐怕很多人都会觉得受害者太傻,就算被骗了感情也不该在一个不知名的平台投钱。
的确如此,但骗子们也早就料到了,他们除了会向受害人展示自己在假平台上的收益,还有一套颇具杀伤力的话术。
“我舅舅是经济学教授,他用凯利公式研究了一套必赢的方法,我用他的方法已经赚了一套房了。
” 
“奥数团队”如果不是破绽,就是骗子的筛选机制但凡留个心眼,去查一查这个“凯利公式”……就中计了,因为你不但发现这个凯利公式是真实存在的,而且还会发现它的确是有关赌博和投资的一个利益最大化策略。
于是,这么一个“凯利公式”就成了让受害者上当的临门一脚。

1818黄金眼采访受骗当事人那么,凯利公式究竟是什么?它真的有所谓的必赢魔力吗? 我们当然要从凯利这个人讲起,他的全名叫小约翰·拉里·凯利,是个美国人。
二战的时候在美国海军当飞行员,战后在得克萨斯大学读了本科和研究生,1953年博士毕业。
凯利的博士论文是做材料研究的,别以后也找了一份比较对口的工作,但并不顺利,没有得到老板的赏识,到他30岁的时候,加入了贝尔实验室。

凯利公式也是他玩出来的一个意外。
当时凯利正在研究电视信号的压缩方法,结果却研究起了赌博来,源头是一档电视答题节目的热播,名叫《64000美元的问题》(The$64000Question)。

节目本身和赌博其实不太相关,最多算是博弈,但因为节目的火爆,有人就开设了赌局,赌的是那个选手能够最终获胜。
可是由于节目在纽约录制,住在美国东海岸的人可以看到实时直播,而西海岸的播出要延后3小时。
因此就有西海岸的赌徒利用电话提前获得了节目信息,利用这种手段作弊赌博。
凯利对此很感兴趣,但是他不是想赢钱,而是希望研究一下这些作弊赌徒如何将利润最大化的问题。
当然,这也说明东西海岸节目播出虽然有3个小时的时间差,但可能停止投注时节目还没有播完,因此赌徒通过电话得知的信息有限的,但足以大大提高胜率。

《64000美元的问题》节目录制现场凯利就针对这种简单的赌局推算出了一种利润最大化的“必赢”公式。
f*=(bp-q)/b,其中f*为计算出来的凯利最优投资比例,b为赔率,即期望盈利/预计亏损,p为成功概率,q为失败概率,即1-p。
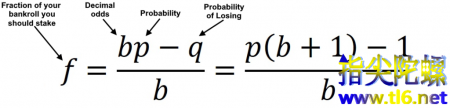
举个最简单的例子,假设一个抛硬币猜正反的简单赌局,每局赌注1元,猜中了得2元,猜错了输掉1元,也就是赔率b=2,胜率p=0.5,带入公式后算得f*=0.25。
也就是说,在这样一个简单的抛硬币赌局中,如果所有的条件都不变,且能够无限次重复的情况下,每次投入所持有本金的25%,可以在不输光本金的前提下实现收益最大化。
同时,凯利公式还有两个隐藏的推论,第一个是只有胜率100%的赌局才值得allin,否则不存在必赢;第二个是只有赌局的期望收益率为正数才能使用凯利公式,否则是不值得投资的,更别提必赢。
凯利的这个研究也引起了香农的兴趣,建议他写成文章发表到杂志上,起初拟的标题为“信息理论与赌博”,但当时AT&T公司的高管认为可能导致大众认为电话业务助长了非法赌博,最终在1956年发表的时候改为了“信息率的新解释”。

老男神克劳德·香农不过这篇文章在发表后其实并没有激起多大的水花,直到一位叫爱德华·索普的赌徒出现。
索普其实也不是普通人,28岁就在麻省理工当教授了,他当时利用职务之便使用早期的计算机IBM704计算了赌博游戏21点的胜率变化。
后来又在香农的建议下读了凯利的文章,了解到了凯利公式这种投资策略,并创造接下来的奇迹。

IBM 704计算机在赌桌上,索普通过记牌的方法来判断胜率,再运用凯利公式来计算自己投注金额,第一次从技术上打败了赌场,在20世纪60年代,索普和一个职业赌徒用一个周末的时间就赢了11000美元(相当于今天约500000美元,以金价计算)。
后来索普把自己的研究和经历写成了畅销书,他出名了也被赌场封杀了,但他后来成为了华尔街成功的对冲基金经理,而凯利公式也顺带进入了大众的视野。

爱德华·索普和他的二十一点研究但实际上,经典的凯利公式并不适用于二十一点游戏,因为二十一点的胜率会随着牌的变化而变化的。
二十一点的规则大多数人应该都了解,简单来说就是手上的牌点数总和不得超过21点,否则爆掉输掉赌注,剩下的点数大的为赢。
赌场的多人游戏中,玩家除了要与其他对手竞争,还要与庄家竞争,而庄家按照规定的策略拿牌,当点数大于17时才停止拿牌,庄家的存在才能让赌场保证赚钱。

二十一点游戏的突破口在于牌库有限索普的突破口就在庄家,当剩余的牌里小点数(2-8点)的牌越少,玩家的优势也就越大,因为庄家很可能会因为拿到大点数的牌而爆掉。
在一些情况下,比如剩余牌的数量较少,且点数较大,玩家的胜率能得到显著的提高,此时才会符合凯利公式中期望收益率为正的前提,但仍然是变化的,只能说索普应用了凯利公式的策略。
总之,凯利公式出名了,或许是最早被赌徒们奉为必胜的秘诀,或许是索普成为对冲基金经理后的成功被人马后炮了,再加上后来流传巴菲特和格罗斯都曾使用凯利公式来投资,也就难免有人把这些归功于数学公式的神奇。

凯利公式(红线)在100次硬币赌局模拟中的收益然而,经典凯利公式只能说给投资者提供了一些策略建议,但现实中的投资行为要比假设的二元赌博游戏复杂得多,盲目套用只会适得其反。
赌博游戏的规则是人为设定的,赔率和胜率都是一致或者可以计算的,并且游戏可以无限次的重复下去。
而现实生活中的投资,比如股票、基金、期货,它们的赔率和胜率不仅未知且难以估算。
另外,简单的二元赌博游戏中,输了会损失本金,而现实中的投资一般并不会完全亏损掉本金,因此凯利公式的一般形式是不能直接套用的。
还有更细节的问题,现实中的单笔交易金额并不一定是可以无限分割的,即便它满足了凯利公式中的条件,也有可能因为剩余资金低于最低交易额,比如股票交易中的一手,就会导致投资无法继续下去,必须注入新的资金。
凯利公式在很多实际投资中并不是必赢的,甚至也不是收益最大的。

有学者做了一个简单的投资模拟,假设有一个投资有60%的概率涨20%,同时有40%的概率跌20%,总体的期望收益率达到4%,算是不错的投资。
套用凯利公式后,得出最佳的投资比例为资金的20%,进行100轮模拟交易后,所得为初始资金的1.98倍,而投资100%和拉了150%杠杆的模型分别为6.24倍和3.36倍。
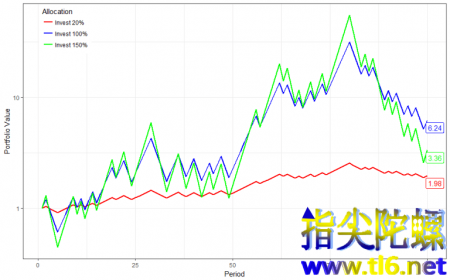
可见凯利公式(红线)的在模拟中的收益并非最大当然在这个简化的投资模拟中,凯利公式的收益更稳定,而后两者的收益和风险也更大,这可能无法反应真实的交易,但也足够说明凯利公式并非万能。
不过话也不能说得太死,在满足条件的游戏或者投资中,严格遵循凯利公式理性投资的话是真的可以稳定获益的,只不过这样期望收益率为正的稳定送钱局,又有哪个憨憨庄家愿意开呢? 别忘了凯利最初的研究针对的可是用电话作弊的赌局,而索普则是用更先进的计算机钻了赌场游戏规则的空子,而大多数普通人只会被骗子钻了情感的空子。