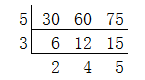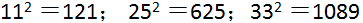缺8æ°
é¿æ³¢ç½å°¼åä¸ä¸è§å½¢ä½å¾
æµè§æ¬¡ä¸è§å½¢ä½å¾é¢ä¸ç»å¸¸åºç°ä¸¤æ¡è¾¹çæ¯å¼ä¸ºp:q(æm:n)è¿ä¸æ¡ä»¶ãäºæ¯æ们å¯è½ä¼æ³å°é¿æ³¢ç½å°¼åï¼å 为é¿æ³¢ç½å°¼åæ¯å°ä¸¤ä¸ªå®ç¹è·ç¦»çæ¯å¼æ¯å®å¼çç¹ç轨迹ãäºæ¯ï¼ä¸é¢ä¸¤é类似é¢ç®ç解æ³å°±é½æå¯è½ç¨å°é¿æ³¢ç½å°¼åãæ们ä¸èµ·æ¥è®¨è®ºä¸ä¸ãä¹å讲ä¸è§å½¢ä½å¾é¢å ±è®²äº15éï¼æ以ï¼ä»å¤©ç两...
1æ3æ¥å1æ6æ¥ç两æï¼å°é¢ä¸æ¯ç¬¬279å280å·ï¼åå«è®²äºä¸¤ç§ç©ºé´å¯éºé®é¢ï¼ â ãæå ³æ£å «é¢ä½ãæ£åé¢ä½çæ趣é®é¢ã â¡ãæ£åé¢ä½ä¸æªè§åé¢ä½å¯ä»¥éºæ»¡ç©ºé´ã 以ä¸ä¸¤æçé¾æ¥å¨æåã æ们ä¸æ说è¿ï¼æäºç§ç¨ææå¾ä½åï¼æï¼é¿åºç±³å¾·ä½éºæ»¡æ´ä¸ªç©ºé´çæ¹å¼ãé¤ä¸é¢ç两ç§å¤ï¼æç®...
以æ°å¦å®¶æ马åªéååå½åçç®æ³è½ç»åºå¾æææçå ¬å¼ï¼ä¸äºå ¬å¼è¯æèµ·æ¥è¿å¾é¾ã ç 究人åæ°æ建çä¸ç§äººå·¥æºè½ï¼AIï¼å¯ä»¥çææ°å¦å ¬å¼ï¼å æ¬ä¸äºæ°å¦å®¶è³ä»é½æ²¡è½è§£å³çé®é¢ã è¿ä¸ªAIåå«æ马åªéæº ï¼RamanujanMachineï¼ ï¼ç 究人åæ³è®©å®ç¨æ°çæ¹æ³è®¡ç®éè¦æ°å¦å¸¸æ°çç²¾ç¡®å¼ ï¼ä¾...
åå 天ï¼è¶ 模å空æäºä¸ä¸ªå 裹ç»8å²è¡¨å¦¹ã ä¸å°ä¸ç§ï¼è¡¨å¦¹å°±ä»å 裹éé¢æ¿åºæ¥ä¸æ¡æ¯æ¯¯ï¼è¡¨å¥ï¼è¿ä¸ªæ¯ç»ç»ç毯å好èæï¼ææ«ç毯ååä½ä¸å¾æåï¼ ä½è¿ä¸ªå¾æ¡æ¯å¥ï¼ä¸æè¶ã å¦æä½ ä¹ä¸æè¿æ¯ä»ä¹ï¼è¯·ç¹å»å¾çï¼è¶ 模åå¬è¯´ï¼å å¿ç¸è£ï¼ä½ä¸ºæè¶ æ¨¡åç表妹ï¼ç«ç¶ä¸æ欧æå ¬å¼ä¸ºä½...
é»ç½æ£æ¸¸æä¸çå¥å¶æ§é®é¢
æµè§æ¬¡æ个æ¯è¾æææçé®é¢ï¼å½¢å¼æ¯è¾å¤ï¼æ说å¼ç¯å ³ç¯çï¼ä¹æ说é»ç½æ£çï¼ä¸è¿é»ç½æ£æ´å®¹æ让å°æåç解ãé»ç½æ£å°±æ¯ä¸é¢æ¯é»æ£ï¼ç¿»ä¸ä¸å°±åæç½æ£ï¼åç¿»ä¸ä¸åååé»æ£ãæ们æ¥ççè¿æ ·çé¢ç®ï¼ 1 æ£çä¸æn个é»æ£ï¼æ¯æ¬¡ç¿»å¨nï¼1个æ£ï¼é£ä¹ç¿»å¨å¤å°æ¬¡ä»¥åï¼n个é»æ£é½åæç½æ£ï¼ è¿...
çé代æ¢æ³çåºç¨
æµè§æ¬¡çæ´»ä¸æå¾å¤ç¸ççéï¼å¦å¹³è¡¡ç天平ã平衡çè··è··æ¿ä¸¤è¾¹çééç¸ç.æ们å¯ä»¥æ ¹æ®è¿äºç¸ççå ³ç³»è¿è¡æ¨çï¼è¿èå¯ä»¥çé代æ¢ï¼æ¾å°çæ¡ã çé代æ¢å ¶å®å¨ä¸å¹´çº§å·²ç»æäºåºæ¬çæ¥è§¦ï¼äºå¹´çº§éï¼æ们æçé代æ¢ä½ä¸ºä¸ç§è§£é¢æ¹æ³æ¿åºæ¥ä»ç»ï¼å¼å¯¼å°æåæ¥å¦ä¹ çé代æ¢ä¸æ¨ççæ¹æ³...
æ¯ä¾å¨å ä½é¢ä¸çåºç¨
æµè§æ¬¡å ä½é®é¢ä¸æ¦ä¸æ¯ä¾é®é¢ç¸ç»åï¼é£ä¹å°±ä¸è¦å纯ç¨æ¯ä¾é®é¢æ¹æ³æ¥è§£å³äºï¼èåºè¯¥ç»åå ä½å¾å½¢æ¥è§£å³ï¼å¾å¾äºåååã 1 å¦ä¸å¾ï¼ABCDæ¯ä¸ä¸ªæ¢¯å½¢ï¼Eæ¯BCçä¸ç¹ï¼ç´çº¿DEæ梯形åæå边形ABEDãä¸è§å½¢CDE两é¨åï¼å®ä»¬çé¢ç§¯ä¹æ¯æ¯10:6ï¼æ±ä¸åºABä¸ä¸åºCDä¹æ¯ã æ们对ä¸å¾æ·»å ä¸æ¡è¾ å©çº¿ï¼...
å ç«å¶åæ¢ ä»å¤©ï¼å æ¾ä¸ªå¨å¾ç»å¤§å®¶ççä»å¤©æç« ç主é¢ï¼ä¸è¦å·çå¦ãããï¼ å·´ææ ï¼ å身å§ï¼ï¼ï¼ å¾çä½è ï¼LucasVB çªç¶åç°èªå·±çå°å¿æ被æ é¢ç»åºåäºï¼å°å¤©ï¼ä½ è¿æ é¢èµ·çç好ãããï¼ è¨å½æ£ä¼ ï¼è¶ 模åä»å¤©è¦è·å¤§å®¶å享çç¡®å®æ¯ å·¥ç§å¤§ç¥å¨ å ç«å¶åæ¢ã 说å°å ç«å¶åæ¢ï¼...
å°éåæ°éµå¾
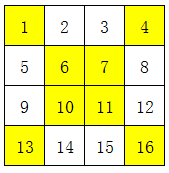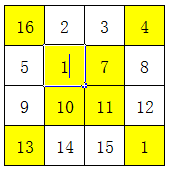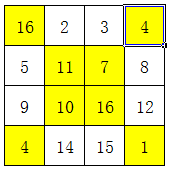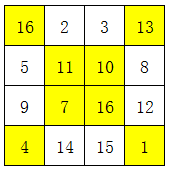
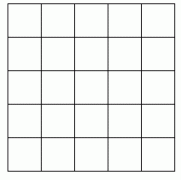
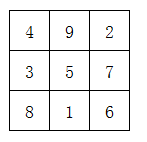
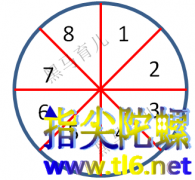
æµè§æ¬¡å°éåæ°éµå¾é常æ¯å¤è¾¹å½¢çæ¯æ¡è¾¹æ¾åæ ·å¤çæ°ï¼ä½¿å®ä»¬çåé½çäºä¸ä¸ªä¸åçæ°ã 1 å¨ä¸å¾ä¸çå°ååä¸å¡«å ¥1~8ï¼ä½¿å¾æ¯æ¡ç´çº¿ä¸ç3个æ°åä¹åé½çäº14ï¼ä¸æ°å1å¿ é¡»å¨å ¶ä¸ä¸ä¸ªè§ä¸ã å°æ°å ³é®ç¹ï¼åä¸ªè§ åªæå个è§ä¸çæ°ä¼è¢«è®¡ç®2次ï¼ä¹å°±æ¯åéå¤1次ã 解é¢æè·¯ï¼ ä¸å¾ä¸çº¿æ¡æ°...
欢快å¦å 为ä½å¤§å£°æ¨å« åå 天ï¼ç«ç¶æ模åç§ä¿¡è¶ 模åï¼è¯´è¿æ¯ä¸æ¯ççã ç½åç§ä¿¡æªå¾WTFï¼ æ°å¦å²ä¸å°±æä¸éå¥è©çé¾é¢ï¼æ¯å代æ°å¦å®¶ä»¬å¨åæé解å³çã åæå¥æ³ 1917å¹´ï¼ä¸ºäºç»æ¥æ¬æ¦å£«å¢æ·»ç活趣å³ï¼æ°å¦å®¶æè°·å®ä¸ï¼KaichibaSoichiKakeyaï¼æåºäºæå³éç æè°·é®é¢ ã æ天ï¼ä¸ä½æ¦...
äºæ¬¡æ²é¢æ¹ç¨åå ¶å¾å½¢
æµè§æ¬¡ä»å¤©ä»ç»äºæ¬¡æ²é¢ï¼ä½ææ³ä»ç´è§ä¸è¿è¡è®²è§£ã ä¸ä¸ªåï¼æ²¿çä¸åæå¨å¹³é¢åç´çæ¹å平移ï¼è½¨è¿¹æ¯ä¸ä¸ªåæ±é¢ã类似å°ï¼æåæ¢ææ¤åãæç©çº¿æåæ²çº¿ï¼ä½åæ ·ç平移ï¼è½¨è¿¹å°æ¯æ¤åæ±é¢ãæç©æ±é¢æåæ²æ±é¢ã æ¤åæ±é¢ãæç©æ±é¢æåæ²æ±é¢ä¹å¯ä»¥ç解为ä¸æ¡è¿æ¤åãæç©çº¿æåæ²...
åå¶æ°é¶å¹»æ¹è§£æ³
æµè§æ¬¡æè°åå¶é¶å¹»æ¹å°±æ¯å½nå¯ä»¥ä¸è½è¢«4æ´é¤æ¶çå¶é¶å¹»æ¹ï¼å³4Kï¼2é¶å¹»æ¹ãæ¯å¦é¤äºäºé¶å¹»æ¹ä»¥å¤ï¼æå°çåå¶æ°é¶å¹»æ¹å°±æ¯å é¶å¹»æ¹äºã åå¶æ°é¶å¹»æ¹çéç¨è§£æ³æ¯è±¡é对称交æ¢æ³ãæ们以ä¸ä¸ªåé¶å¹»æ¹ä¸ºä¾ï¼å ¶å ·ä½æä½æ¥éª¤å¦ä¸ï¼ 1.å°å¹»æ¹åæ22ç4个åºåï¼ç±äºæ¯åå¶æ°é¶å¹»æ¹ï¼æ以è¿...
å¹³åæ°å¯èï¼å æç®æ°å¹³å
æµè§æ¬¡ä¸æ¬¡ä»ç»äºä¸ä¸ç®åç®æ°å¹³åï¼å°±æ¯ææææ°åæ±åï¼é¤ä»¥æ°åç个æ°ãä½æ¯ææ¶åä¼æ¶åå°æ°åçåç»è®¡ç®ï¼è¿ä¸ªæ¶åå½ç¶å°±éå使ç¨å æç®æ°å¹³åäºï¼å ¶å®å æç®æ°å¹³åçæ¬è´¨è¿æ¯ç®æ°å¹³åï¼åªä¸è¿æç¸åçæ°åç´æ¥ä¹ä»¥è¿ä¸ªæ°åç个æ°ï¼æéï¼ï¼ä»¥å¿«éæ±åã å æç®æ¯å¹³åæ°ç计ç®...
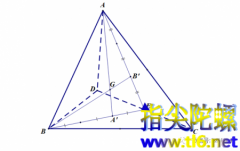
åé¢ä½çè´¨å¿å¨åªå¿ï¼
æµè§æ¬¡ä»å¤©è®²ä¸ä¸ªç®åçç¥è¯ï¼é£å°±æ¯åé¢ä½çè´¨å¿ï¼ä¹å«åéå¿æä¸å¿ï¼ãæ们è¦è¯æä¸ä¸ªåé¢ä½æ¯ä¸ªé¡¶ç¹å°å¯¹é¢ä¸å¿è¿çº¿ï¼å«ååé¢ä½çä¸çº¿ï¼ç¸äº¤äºä¸ç¹ï¼ä¸è¿ç¹å°é¡¶ç¹è·ç¦»ä¸å°å¯¹é¢ä¸å¿è·ç¦»ä¹æ¯ä¸º3:1ã æ们ç¥è¯ï¼å¨å¹³é¢æ¶ï¼ä¸è§å½¢ä¸æ¡ä¸çº¿ç¸äº¤äºä¸ç¹ï¼è¿ç¹å«åè´¨å¿ï¼æéå¿ãä¸å¿ï¼ï¼...
åå¶æ°é¶å¹»æ¹è§£æ³
æµè§æ¬¡æè°åå¶é¶å¹»æ¹å°±æ¯å½nå¯ä»¥è¢«4æ´é¤æ¶çå¶é¶å¹»æ¹ï¼å³4Ké¶å¹»æ¹ãå¨è¯´è§£æ³ä¹åæ们å 说æä¸ä¸ªäºè¡¥æ°å®ä¹ï¼å°±æ¯å¨né¶å¹»æ¹ä¸ï¼å¦æ两个æ°çåçäºå¹»æ¹ä¸æ大çæ°ä¸æå°æ°çåï¼å³nnï¼1ï¼ï¼æ们称å®ä»¬ä¸ºä¸å¯¹äºè¡¥æ°ãå¦å¨1~9çä¸é¶å¹»æ¹ä¸ï¼æ¯ä¸å¯¹å为10çæ°ï¼æ¯ä¸å¯¹äºè¡¥æ°ï¼å¨1~16çåé¶å¹»...
åç«æ¹ä½çå¶ä½
æµè§æ¬¡ä»å¤©è®²ä¸ä¸ªå¾æ趣ä¹å¾å®é çé®é¢ï¼æ¨è¥æå ´è¶£ä¹ææ¡ä»¶ï¼å¯ä»¥ç¨æ¨åæå ¶ä»ææèªå·±å¨æå¶ä½ã æ两个棱é¿ä¸º1åç±³ï¼10åç±³ï¼çæ£æ¹ä½æ¨åï¼å¹¶ä¸æ们è¿æä¸æ ¹æ¨æï¼å®çé¿åº¦æ¯ 请æ¨ç¨è¿ä¸¤ä¸ªæ£±é¿ä¸º1åç±³çæ¨å为ææï¼å¯¹å®ä»¬è¿è¡åå²åæ¼æ¥ï¼èæ为ä¸ä¸ªæ£æ¹ä½ãè¦æ±åä¸æ¥çååæ¼æ¥...
ï¼1ï¼åå¤ä¸ä¸ªæ£åé¢ä½ï¼å ç¡®å®åºå®æ¯æ¡æ£±ä¸ç两个ä¸çåç¹ãé£ä¹ï¼ä¸æ个顶ç¹ç¸é»çä¸çåç¹å°±æä¸ä¸ªï¼ä¸å¾ä¸ç¨åä¸é¢è²è¡¨ç¤ºï¼ï¼ç¨ä¸ä¸ªè¿è¿ä¸ç¹çå¹³é¢æä¸ä¸ªè§ï¼ä¸é¢è§ï¼æªå»ï¼æç å»ï¼ãæ£åé¢ä½æå个ä¸é¢è§ï¼é½è¿æ ·ç å»ï¼ä¾¿å¾å°æè°çé¿åºç±³å¾·ä½ä¹ä¸æªè§åé¢ä½ãä¸é¢ä¸¤å¾...
å¥æ°é¶å¹»æ¹è§£æ³
æµè§æ¬¡å¥æ°é¶å¹»æ¹æç»å ¸çå¡«æ³æ¯ç½ä¼¯ç¹æ³ï¼ä¹æå¦å¤ä¸ä¸ªæ¯è¾éä¿çå«æ³æ¥¼æ¢¯æ³ã该æ¹æ³ä¸ºï¼ 1.æè¿ä¸ç³»åæ°ä¸æç §ä»å°å°å¤§ç次åºæåï¼ç¶åå°ç¬¬ä¸ä¸ªæ°ï¼æå°çæ°ï¼æ¾å¨ç¬¬ä¸è¡çä¸é´ï¼å©ä½æ¯ä¸ä¸ªæ°é½æ¾å¨åä¸ä¸ªæ°çå³ä¸ä¸æ ¼ï¼ 2.å¦æè¿ä¸ªæ°è¦æ¾çæ ¼å·²ç»è¶ è¿äºé¡¶è¡ï¼é£å°±æå®æ¾å°åºè¡ï¼ä½...
è¿æ¯ä¸ä¸ªæ趣çé®é¢ï¼å®æ¾ç»æ¯ä¸éç«èµé¢ï¼ä½æ åçæ¡å´æ¯é误çãä¸ä½å°èçæåºäºé误ï¼è¯å§ä¸å¾ä¸æ¹å¤è¿ä½èçæ£ç¡®ãå ·ä½æ¥è¯´ï¼é¢ç®æ¯ï¼æä¸ä¸ªæ£å棱é¥ï¼åºé¢ä¸ºæ£æ¹å½¢çç´æ£±é¥ï¼ï¼å个侧é¢é½æ¯æ£ä¸è§å½¢ï¼å¦æä¸ä¸ªæ£åé¢ä½ï¼å®çä¸è§å½¢é¢ä¸æ£å棱é¥ç侧é¢ä¸æ ·å¤§å°ãè¥æè¿ä¸¤...
ç®åå¹»æ¹ç解æ³å£è¯
æµè§æ¬¡å ³äºå¹»æ¹ï¼æ们å¨ããå年级ã认è¯å¹»æ¹ãä¸å·²ç»ä»ç»è¿ï¼è¿éå°±ä¸éå¤è¯´äºï¼ä»å¤©ä¸»è¦æ¯ä»ç»ä¸ä¸å¤äººå¯¹ä¸é¶å¹»æ¹çä¸ç§å·§å¦åæ³ã å¤ä»£å¯¹ä¸é¶å¹»æ¹åå«åä¹å®«ï¼æå½åå®èåæ°å¦å®¶æ¨è¾æ¾å¯¹ä¹è¿è¡è¿ç²¾å¿ç 究ãå¨ä»æèçãç»å¤æå¥ç®æ³ãä¸ï¼ååºäºä¸ç§ååå·§å¦ç解æ³ï¼å ¶å£è¯æ¯ï¼...
ç´çº¿ååï¼æå¤å åï¼
æµè§æ¬¡å ¶å®æ´å¥½ç©çé¢ç®æ¯å西çï¼ä¸è¿å¤ªç«ä½äºï¼å¯¹äºäºå¹´çº§çæ¥è¯´ï¼å æ¥ç©ç©ç´çº¿ååï¼æè 说æ¯ååå饼ãè·ç´çº¿ç¸äº¤ä¸æ ·ï¼å¦ææ¯å交ç¹é½å¨ä¸èµ·ï¼é£ä¹æ¯ä¸åé½ä¼å¢å 2åï¼2å4åã3å6åã4å8åï¼æ¯å¦ï¼ è·ç´çº¿äº¤ç¹ä¸æ ·ï¼æ们ä¸è¬æ¯æ±ä¸ååä¸å»ï¼æå¤è½åæå¤å°åãæ们ç°å¨è¯è¯ï¼...
æå°å ¬åæ°æä¹æ±ï¼
æµè§æ¬¡åºæ¬æ¦å¿µ æå°å ¬åæ°ï¼å 个æ°å ¬æçåæ°ï¼å«åè¿å 个æ°çå ¬åæ°ï¼å ¶ä¸æå°çï¼å°±å«åæå°å ¬åæ° æå°å ¬åæ°çæ±æ³ä¹æå¾å¤ç§ï¼éè¦æ ¹æ®æ åµçµæ´»è¿ç¨ã 1 çé¤æ³ çé¤æ³æ们å¨æ±æå¤§å ¬çº¦æ°çæ¶åå·²ç»å¦ä¹ è¿ï¼å°±æ¯å ç¨è¿å 个æ°çå ¬çº¦æ°è¿ç»å»é¤ï¼ ä¸ç´é¤å°å两两äºè´¨ä¸ºæ¢ ï¼æ³¨æï¼...
ç´çº¿ç¸äº¤ï¼å¤å°äº¤ç¹ï¼
æµè§æ¬¡è¿æ¯ä¸ªæææçé®é¢ï¼ä¸¤æ¡ç´çº¿ç¸äº¤ï¼å¤å°ä¸ªäº¤ç¹ï¼é£è¯å®åªæä¸ä¸ªå¯¹ä¸å¯¹ï¼åæ¡ç´çº¿å¢ï¼å½ç¶æå°ä¹åªæä¸ä¸ªï¼åªè¦è¿åæ¡ç©¿è¿ä¸ä¸ªç¹ç¸äº¤å³å¯ï¼æ¯å¦ï¼ å¯è§ï¼æ±æå°äº¤ç¹æ²¡å¤ªå¤§æä¹ï¼æ以æ们ä¸è¬æ¯æ±æå¤æå¤å°ä¸ªäº¤ç¹ãæ们ç°å¨å·²ç»ç¥éï¼ â ä¸æ¡ç´çº¿ï¼æå¤0个交ç¹ï¼ â¡ä¸¤æ¡ç´çº¿ç¸...
æå¤§å ¬çº¦æ°çåºç¨
æµè§æ¬¡åªæ¯æ±å 个æ°çæå¤§å ¬çº¦æ°ï¼ä¸æ¬¡å·²ç»æè¿å ç§ä¸åçæ¹æ³ï¼ä½æ¯å¦ä½ä»ä¸ä¸ªåºç¨é¢æ³å°å»æ±æå¤§å ¬çº¦æ°ï¼éè¦æ´å¤çè®ç»ã 1 ä¸å¼ é¿æ¹å½¢ç纸ï¼é¿2703åç±³ã宽1113åç±³ï¼å¦ææè¿å¼ 纸è£æè¥å¹²ä¸ªåæ ·å¤§å°çæ£æ¹å½¢ï¼çº¸å¼ ä¸å 许æå©ä½ï¼éè¦æ°å¥½ä½¿ç¨å®ï¼é£ä¹è¿æ ·çæ£æ¹å½¢æ大边é¿æ¯å¤å°å...
èªç¶çä¸æä¸å°ç¥å¥ç°è±¡ä»¤äººéæ¼ï¼ä½ è½æ³å°èå·¢ãè¥ç泡å海绵å¤éª¨éª¼ä¹é´çå¥å¦èç³»åï¼çæ¡æ¯å®ä»¬éç±å 边形ã为ä½èèä¼æé åºå®ç¾çå 边形èå·¢ï¼è¿å½ç¶ä¸æ¯ä»ä¹ç¥ç§çåéï¼èæ¯å ¶ä¸å¯å«çæ·±å»æ°å¦åç©çå¦éçã èèï¼å¤©ççæ°å¦å®¶ï¼ èå·¢ç®ç´æ¯ä¸ªå·¥ç¨å¦å¥è¿¹ï¼å®ç±ä¸ææ...
ä»ä¹æ¯æå¤§å ¬çº¦æ°ï¼ åºæ¬æ¦å¿µ æå¤§å ¬çº¦æ°ï¼å 个æ°å ¬æç约æ°ï¼å«åè¿å 个æ°çå ¬çº¦æ°ï¼å ¶ä¸æ大çï¼å°±å«åæå¤§å ¬çº¦æ°ï¼ äºè´¨æ°ï¼å¦æ两个æ°çæå¤§å ¬çº¦æ°æ¯1ï¼é£ä¹è¿ä¸¤ä¸ªæ°å«åäºè´¨æ° æå¤§å ¬çº¦æ°çæ±æ³æå¾å¤ç§ï¼å¸¸è§çæè´¨å æ°å解æ³ãçé¤æ³ãè¾è½¬ç¸é¤æ³ãæ´ç¸åææ³ï¼éè¦æ ¹æ®...
大å¦é带é¥ä¹é£çè¡ï¼é¿æä¸æè¿åç°ï¼ä»¥åçäºä¸¤é¥é½åä¸å®ï¼ç°å¨æä¹ä¸ä¸¤é½åä¸é¥±å¢ï¼äºæ¯å¯¹è¿ä¸ªé£å é¿å§¨çæé¥ææ¯æ·±è¡¨æç ç¥å¥ç两 两ï¼ä½ä¸ºä¸å½ç¹æçééåä½ï¼å¨ä¸å½åå²ä¸æçå¾éè¦çå°ä½ï¼å°æ¶åç»å¸¸çæ°´æµï¼éé¢æ¶å¸¸ä¼åºç°å°äºï¼äºä¸¤çèçç»é¢ã é£ä¹ä¸¤è¿ä¸ç¥å¥ç...
å¹³æ¹æ°ä¸è´¨å æ°çææ°
æµè§æ¬¡ä¸ä¸ªèªç¶æ°å¹³æ¹åï¼å¾å°çæ°å«åå¹³æ¹æ°ï¼æè å®å ¨å¹³æ¹æ°ãæ¯å¦ï¼ è¿éç121ã625ã1089å°±æ¯å¹³æ¹æ°ï¼æ们æå¹³æ¹æ°å解质å æ°ä»¥åè§å¯ä¸ä¸ï¼ æ们å¯ä»¥è§å¯åºæ¥ï¼åè´¨å æ°çææ°é½æ¯å¶æ°ï¼æ以æ以ä¸ç»è®ºï¼ ç»è®º ä¸ä¸ªå¹³æ¹æ°å解质å æ°ä»¥åï¼åè´¨å æ°çææ°é½æ¯å¶æ°ï¼ åä¹ï¼å¦æä¸ä¸ªæ°...
çå·®æ°åæ±åçå·§ç®
æµè§æ¬¡çå·®æ°åæ±åå ¬å¼æ¯è¾å¥½ç¨ï¼ä½æ¯å¨æäºé¢ç®ä¸ï¼ç´æ¥è¿ç¨æ±åå ¬å¼ä¹æ¯è¾éº»ç¦ï¼å¯ä»¥éå以ä¸å·§ç®çæå·§ã ä¾ ä»1å°2020çææèªç¶æ°ä¸ï¼ææå¶æ°ä¹åï¼åå»å¥æ°ä¹åï¼ç»ææ¯å¤å°ï¼ 1å°2020çèªç¶æ°åï¼æ»å ±2020个æ°ï¼å ¶ä¸ï¼å¶æ°é¡¹1010个ï¼2å¼å¤´ã2020ç»å°¾ï¼å ¬å·®æ¯2ï¼å¥æ°é¡¹1010个ï¼1å¼å¤´ã...
å å¼å解å¨æ¾è§å¾ä¸çåºç¨
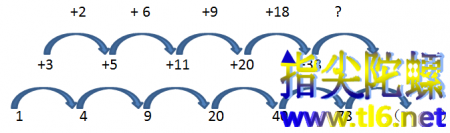
æµè§æ¬¡ä¸æ¬¡ä»ç»è¿æ¡¥ä¸ææ¡¥ï¼æ¯åº§æ¡¥ä¸çè§åå®å ¨ä¸ä¸æ ·ï¼å¦å¤è¿æä¸ç§ï¼æ¯å°æ°åå å¼å解åï¼æ¯ä¸ªå ååèªæåèªçè§å¾ã 第ä¸é¢ï¼1ã4ã9ã20ã40ã78ãï¼ï¼ è¿æ¯èåæ³ï¼å¨ç´æ¥è§å¯çä¸åºæ°åä¹é´è§å¾ï¼ä¹ä¸åå¨è·å¹³æ¹ãç«æ¹ç¸å ³çæ¶åï¼æ们è¿æ¯å¨æ¯ä¸¤ä¸ªæ°åä¹é´æä¸åº§æ¡¥ï¼å¹¶å¨æ¡¥ä¸æ ...